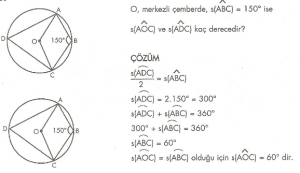
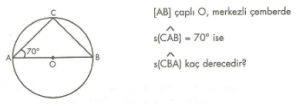
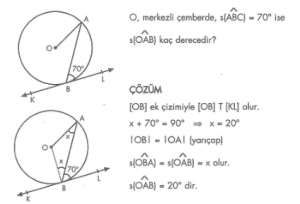
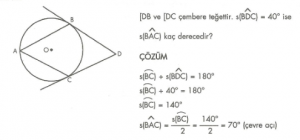
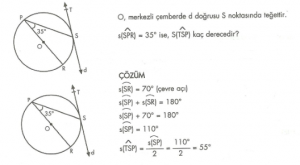
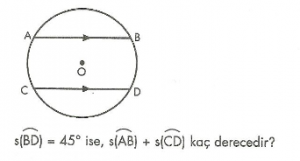
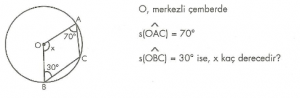
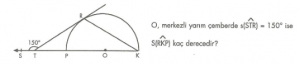
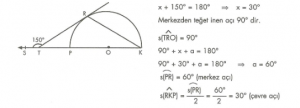
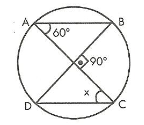
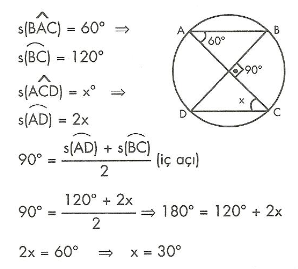
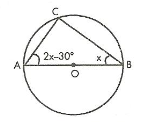
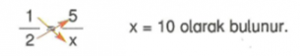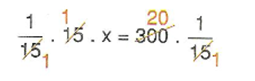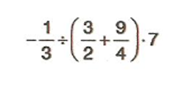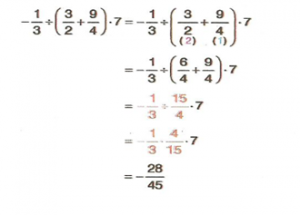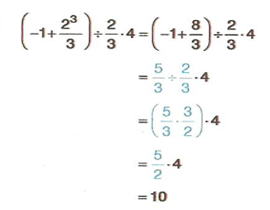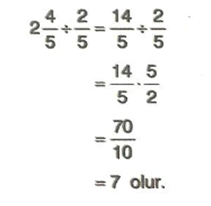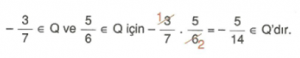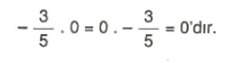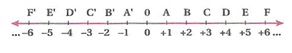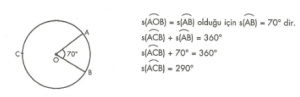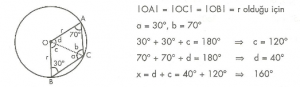7. Sınıf Matematik Oran ve Orantı Konu Anlatımı
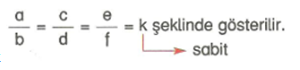
Oran Orantı
İki çokluğun karşılaştırılmasına oran, iki oranın eşitliğine orantı denir.
Örnek : Mert’in boyu 155 cm, kardeşininki 140 cm ise kardeşinin boyunun, Mert’in boyuna oranını bulalım.
Çözüm : Kardeşinin boyu/Mert’in boyu = 140/155 = 28/31’dir.
Örnek : 3/5 = 9/15 ifadesi bir orantı mıdır?
Çözüm :  olduğundan bu bir orantıdır.
olduğundan bu bir orantıdır.
Orantı Çeşitleri
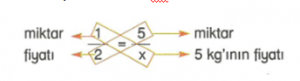
1 kg elma 2 TL ise 5 kg elma aldığımızda kaç TL ödeneceğini miktar ve fiyata bağlı olarak tabloda gösterelim.
Miktarın fiyata oranı 1/2 ‘dir.
Orantıda terimlerin çapraz çarpımı birbirine eşittir.
1 . x = 2. 5
X = 10
Aynı sonuç kesirlerin denkliğinden yararlanarak da bulunur.
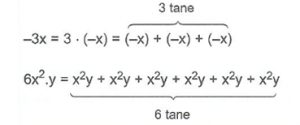
- Doğru Orantı : Bir orantıdaki iki çokluktan biri 2, 3, 4, … kat artarken diğer çokluk da 2,3,4, … kat artıyorsa ya da biri belli oranlarda azalırken diğeri de aynı oranda azalıyorsa bu orantıya doğru orantı denir. X ve y birer değişken olmak üzere aralarında y = mx bağıntısı vardır.
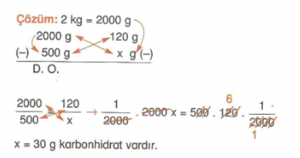
Örnek : 2 kg yoğurtta 120 g karbonhidrat bulunmaktadır. Aynı yoğurdun 500 g’ında kaç gram karbonhidrat vardır.
- Ters Orantı : Bir orantıdaki iki çokluktan biri 2, 3, 4, … kat artarken diğer çokluk 2, 3, 4, … kat azalıyorsa bu orantıya ters orantı denir. X ve y birer değişken olmak üzere aralarında x.y=m bağıntısı vardır.

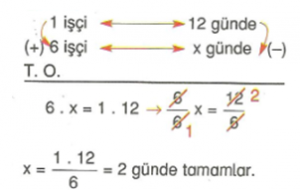
Örnek : Bir işçi bir işi tek başına 12 günde tamamlıyor. Aynı koşullarda aynı işi 6 işçi kaç günde tamamlar?
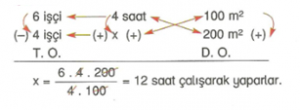
- Bileşik Orantı
Değerleri eşit üç veya daha fazla orandan oluşan orantıya bileşik orantı denir.
Örnek : 6 işçi günde 4 saat çalışarak 100 m2 kaldırım döşemektedir. Aynı hızla çalışan 4 işçi 200 m2 kaldırım döşemesini günde kaç saat çalışarak yaparlar?
- Aynı birimler alt alta yazılır.
- Üçlü orandan biri kapatılarak diğerlerinin artıp azalmasına göre orantı çeşidi yazılır.
- Ters orantı ile bilinmeyenin üstündeki sayı; doğru orantının altındaki sayı işaretlenir.
- İşaretlenen sayılar çarpılıp diğerlerine bölünürse bilinmeyen bulunur.
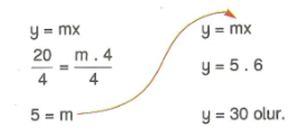
Örnek : x ile y doğru orantılıdır. X = 4 iken, y = 20 ise, x = 6 iken, y kaç olur?
Çözüm : Doğru orantılı olduğundan y = mx’dir.
Yerine değerleri yazılırsa orantının sabiti bulunur. Cümlenin ikinci yarısında sabit sayı yazılarak y bulunur. Şöyle ki;
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik Denklemler Konu Anlatımı
Denklemler
Birinci Dereceden Bir Bilinmeyenli Denklemler
İçinde bilinmeyen bulunan ve bilinmeyenin aldığı değere göre doğruluğu sağlanan cebirsel ifadelere denklem denir. İçinde bir bilinmeyen bulunan ve bilinmeyenin derecesi 1 olan denklemlere birinci dereceden bir bilinmeyeli denklem denir.
Denklemin doğruluğunu sağlayan değerini bulmaya denklemi çözmek denir.
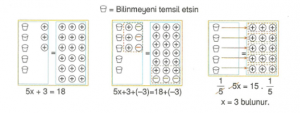
Örnek : 5x + 3 = 18 denklemini sayma pulları ile modelleyelim.
Çözümün doğruluğunu kontrol edelim.
5x + 3 = 18’de x yerine 3 yazalım.
5 . 3 + 3 = 18
15 + 3 = 18
18 = 18 olduğundan çözüm doğrudur.
5x + 3 = 18 denklemini çözümleyelim.
5x + 3 + (-3) = 18 + (-3) Bir eşitliğin her iki yanı (-3) ile toplanırsa eşitlik değişmez.
5x + 0 = 15 “0 (sıfır)” toplamada etkisiz eleman
X = 3 sonucu bulunur.
Ç = {3} veya Ç = {x = 3} olur.
Denklem çözümündeki kurallar
- Bir eşitliğin her iki yanı aynı sayı ile toplanır ya da çıkarılırsa eşitlik değişmez.
- Bir eşitliğin her iki yanı aynı sayı ile çarpılır ya da bölünürse eşitlik değişmez.
Not: Denklemler problem çözümünde kolaylık sağlar. Problem denklemle anlamlandırılarak çözümlenir.
Problem : Cem harçlığında her ay 15 TL biriktirmeye karar veriyor. Cem 300 TL’yi kaç ayda biriktirir?
Çözüm : Problemde bilinmeyene x diyerek soruyu denklemle ifade edelim.
Cem 1 ayda 15 TL biriktiriyorsa x ayda 300 TL biriktirir.
15 . x = 300 denklemiyle ifade edip çözersek;
X = 20 ay bulunur.
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik Örüntüler ve İlişkiler Konu Anlatımı
Örüntüler ve İlişkiler
- Kesme ile 2 tane parça -> 21
- Kesme ile 4 tane parça -> 22
- Kesme ile 8 tane parça -> 23
- Kesme ile 16 tane parça -> 24
. .
. .
- kesme ile 2 tane parça 2n parça oluşur.
2 sayısının n defa kendisiyle çarpılmasıyla elde edilen 2 n ifadesi bir üslü ifadedir. Burada 2 taban, n üs (kuvvet) olarak isimlendirilir.
Örneğin, 25 = 2 X 2 X 2 X 2 X
33 = 3 X 3 X 3
74 = 7 X 7 X 7 X 7
106 = 10 X 10 X 10 X 10 X 10 X 10
42 = 4 X 4
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik Cebirsel İfadeler Konu Anlatımı
Cebirsel İfadeler
Etkinlik
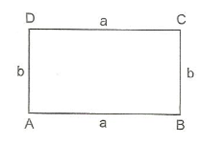
Kenar uzunlukları a ve b birim olan ABCD dikdörtgenin çevresini 2a + 2b, alanını ise a. b ile ifade edebiliriz.
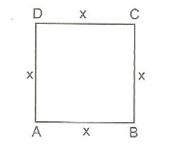
Aynı şekilde, bir kenar uzunluğu x birim olan yandaki ABCD karesinin çevresi 4 . x , alanı x . x = x2 dir.
Yukarıda verdiğimiz örneklerde olduğu gibi anlatmak istediğimiz bir ifadeyi harfler (bilinmeyenler) yardımıyla göstermeye cebirsel ifade denir.
Örnek : 4x, 5a2, 1/3 x.y, -2x3y.z, πr2 … gibi
Not : Matematikte kullanılan bazı sabitlerle cebirsel ifadeler karıştırılmamalıdır. Harfli ifadeler, içinde bulunan değişkenin alacağı değere göre farklı değerler alır; sabitler ise değişmez.
Örneğin, π (pi) sayısı.
Terim : Bir cebirsel ifadede toplama ya da çıkarma yoluyla birbirinden ayrılan ifadelerin her birine terim denir.
Örnek : 3x2 + 4x – 8 ifadesinde 3x2, 4x, 8 ifadelerinin her biri terimdir. Bu ifadede üç terim vardır.
Not : Bir cebirsel ifadede yanında bilinmeyen bulunmayan ifadeye sabit terim denir.
4x3 – 27 ifadesinde (-27) sabit terimdir.
Sizde;
5a + 8x + 9y2 – 13y + 1/3 x3
İfadesinde kaç terim olduğunu, terimleri ayrı ayrı yazarak ve arkadaşlarınızla da tartışarak bulunuz.
Derece : Bir cebirsel ifadede herhangi bir bilinmeyenin kendisiyle kaç defa çarpılacağı gösteren ve bilinmeyenin sağ üst köşesine yazılan sabit sayıya derece denir. Derecesi en yüksek terimin derecesi, cebirsel ifadenin derecesini verir.
Örnek : 4y4 + 3x3 – 5z ifadesinde y nin derecesi 4’tür. En yüksek derece y’nin derecesi olduğundan ifade 4. derecedendir denir.
Katsayı : Cebirsel ifadelerde toplama ya da çıkarma yoluyla ayrılan terimlerin yanında çarpım olarak bulunan sabit sayılara katsayı denir.
Örnek : 16x – 25y2 . z ifadesinde x’in katsayısı 16; y2.z nin katsayısı (-25)’tir.
Not : Reel sayılar kümesi çarpma işlemine göre değişme özelliğine sahip olduğundan katsayı bilinmeyen ifadenin solunda ya da sağında olması ifadenin değerini değiştirmez, ancak işlem kolaylığı açısından katsayı genellikle soluna yazılır.
Katsayı, bir ifadenin kendisiyle kaç defa toplanacağını gösterir.
Benzer Terim : Bir cebirsel ifadede aynı dereceli terimlere benzer terim denir.
Örnek : 8x + 16X – 2/3 y2 + 5y2 cebirsel ifadesinde
8x ile 16x, -2/3 y2 ile 5y2 benzer terimlerdir.
Kategoriler: Matematik Etiketler:
7.Sınıf Matematik Rasyonel Sayılarla Adım Adım İşlemler Konu Anlatımı
Rasyonel Sayılarla Adım Adım İşlemler
Birden fazla işlem olduğu durumlarda;
Önce üslü sayılar,
Sonra parantez içindeki işlemler,
Daha sonra çarpma veya bölme işlemleri,
En son olarak da toplama veya çıkarma işlemleri yapılır.
Uyarı : Aynı önceliğe sahip işlemlerde soldan sağa doğru sıra takip edilir.
işleminin sonucunu bulalım.
Örnek : 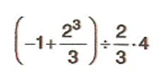 işleminin sonucunu bulalım.
işleminin sonucunu bulalım.
Örnek : Bir sürahi 2 4/5 litre meyve suyu alıyor.
Bir barda 2/5 litre meyve suyu aldığına göre, sürahideki meyve suyunun kaç bardak geldiğini bulalım.
Çözüm : Sürahideki meyve suyunun kaç bardak geldiğini bulmak için sürahinin hacmini bir bardağın hacmine bölelim.
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik Rasyonel Sayılar Konu Anlatımı
Rasyonel Sayılar
Sayı doğrusu üzerinde; ardışık tam sayılar arasında açıkta kalan çok sayıda nokta vardır. Bu noktaların bazılarına karşılık gelen sayılar, farklı bir küme oluşturur ve aşağıdaki gibi tanımlanır.
a ve b tam sayı, b ≠ 0 olmak üzere, a/b biçiminde yazılabilen sayılara rasyonel sayılar denir. Rasyonel sayılar kümesi “Q” ile gösterilir.
Q = { …, – 3/2, -1, -3/5, 0, 1/2, 3/4, …}
Rasyonel sayılar kümesi; negatif rasyonel sayılar, pozitif rasyonel sayılar ve 0 (sıfır) dan oluşur.
Q = Q– ∪ {0} ∪ Q+
N ⊂ Z ⊂ Q dur.
Her tam sayı, paydası 1 olan rasyonel sayıdır.
Bir bütün 4 eş parçaya bölünürse;
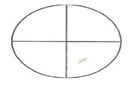 taralı kısım ¼ sayısı ile ifade edilir.
taralı kısım ¼ sayısı ile ifade edilir.
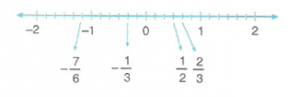
Örnek :
-1/3, 2/3, -7/6, ½ rasyonel sayılarını sayı doğrusunda gösterelim.
Alıştırmalar
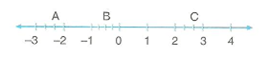
- Aşağıda verilen sayı doğrusuna göre, A, B ve C noktalarına karşılık gelen rasyonel sayıları bulunuz.
- Sayı doğrusundaki balonların içine yazılması gereken rasyonel sayıları aşağıdakilerden seçerek yazınız.
-4/3, 4/5, 1/2, 7/2, -1/2
Rasyonel Sayılarla Toplama ve Çıkarma Konu Anlatımı
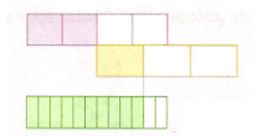
Şekilde modellenen toplama işlemine ait matematik cümlesi;
2/4 + 1/3 = 10/12’dur.
Şekilde modellenen çıkarma işlemine ait matematik cümlesi;
5/8 – 3/8 = 2/8’dir.
Sayı doğrusundaki matematik cümlesi;
6/12 + 4/12 = 10/12’dur.
Sayı doğrusundaki matematik cümlesi;
5/8 – 3/8 = 2/8’dir.
Örnek : 3 2/5 ile (-3/4) tam sayılı kesir bileşik kesre çevilir.
=(68/20) + (-15/20) paydaları eşittir.
=68-15 / 20 ortak paydaya yazılır.
= 53/20 = 2 13/20 sonuç bulunur.
Rasyonel sayılarda toplama işlemi yapılırken;
- Tam sayılı kesir, bileşik kesre çevrilir.
- Paydalar eşit değilse eşitlenir.
- Ortak paydaya yazılır.
- Paylar toplamı paya yazılarak sonuç bulunur.
- Sonuç en sade şekilde bırakılır.
Rasyonel Saylarla Çarpma ve Bölme Konu Anlatımı
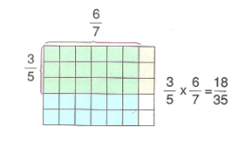
Kesirlerle Çarpma İşlemi
3/5 ile 6/7 kesirlerini modelleyerek çarpalım.
Rasyonel Sayılarla Çarpma İşlemi
Örnek :  rasyonel sayılarının çarpımlarının sonucunu önce tahmin edelim.
rasyonel sayılarının çarpımlarının sonucunu önce tahmin edelim.
Sonra işlem sonucu ile tahminimizi karşılaştıralım.
Tahmin : -3
İşlem Sonucu : -2,7
Rasyonel sayılarla çarpma işlemi yaparken;
- Tam sayı ve tam sayılı kesir varsa bileşik kesre çevrilir.
- Paylar kendi aralarında, paydalar kendi aralarında çarpılacak şekilde yazılır.
- İşaretleri çarpılır.
- Varsa sadeleştirmeler yapılarak sonuç bulunur.
1. Q’da çarpma işleminin kapalılık özelliği vardır.
- Örnek :
2. Q’da çarpma işleminin değişme özelliği vardır.
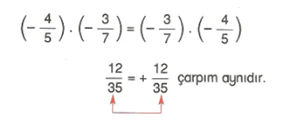
3. Q’da çarpma işleminin etkisiz (birim) elemanı 1’dir. Etkisiz (birim) eleman e ile gösterilirse e = 1 ‘dir.

4. Q’da çarpma işleminin yutan elemanı 0 (sıfır) dır. Sıfırın herhangi bir sayı ile çarpımı sıfırdır.
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik Tam Sayılar Konu Anlatımı
Tam Sayılar
Günlük yaşantımızda bazı kavramları ifade etmek için doğal sayılar yeterli değildir.
Sıfırdan küçük sayılara da ihtiyaç vardır.
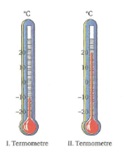
Mesela aşağıdaki termometreleri inceleyelim.
- termometrede sıcaklık sıfırın altında 10 C (ya da – 10 C)
- termometrede sıcaklık sıfırın üstünde 20 C (ya da – 20 C) dir.
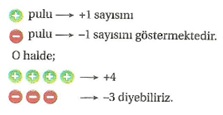
Sıfırın altındaki sıcaklıkların önüne (-), sıfırın üstündeki sıcaklıkların önüne (+) işareti konulur.
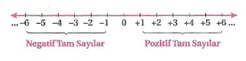
Sıfırdan büyük olan tam sayılara pozitif tam sayılar denir ve Z+ ile gösterilir.
Z+ = {+1, +2, +3, ……}
Sıfırdan küçük olan tam sayılara negatif tam sayılar denir ve Z– ile gösterilir.
Z– = {…….., -3, -2, -1}
Not : Tam sayılara aynı zamanda yönlü sayılar da denir. Bir yön pozitif (+) olduğunda, bu yönün tersi negatif (-) olur.
Örnek – 1
Bir ailenin aylık geliri 1000 TL -> +1000 TL
Bir ailenin aylık gideri 700 TL -> -700 TL
Bir malın satışından elde edilen
80 TL kar -> +80 TL
Bir malın satışından edilen
35 TL zarar -> -35 TL
Deniz seviyesinin 40 m altı -> -40m
Deniz seviyesinin 20 m üstü +20m
Not : Sıfırın işareti yoktur. Yani “0” ne negatif ne de pozitiftir.
O halde tam sayıları tanımlayacak olursak;
Negatif tam sayılar, “0” ve pozitif tam sayıların oluşturduğu kümeye tam sayılar kümesi denir ve Z ile gösterilir.
Z = Z– ∪ {0} ∪ Z+
Z 0 {…, -3, -2, -1, 0, 1, 2, 3, …}
Her tam sayıya, sayı doğrusu üzerinde bir nokta karşılık gelir ve bu noktaya o tam sayının görüntüsü denir.
Sıfır sayısının görüntüsü olan “0” noktası da başlangıç veya referans noktası denir.
Tam Sayılarda Toplama Çıkarma Konu Anlatımı
Tam Sayılarda Toplama İşlemi
- Pullarla Toplama İşlemi
Örnek : Erzurum’da hava sıcaklığı +4 C dir.
Erzurum’da hava sıcaklığı 2 C artarsa sıcaklığın kaç derece olduğunu bulalım.
Çözüm :
Erzurum’da hava sıcaklığı +6 C olur.
Örnek : Ardahan’da hava sıcaklığı -5 C dir.
Hava sıcaklığı 4 C azalırsa son durumda Ardahan’da sıcaklığın kaç derece olacağını bulalım.
Çözüm :
Ardahan’da hava sıcaklığı -9 C olur.
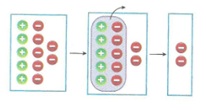
Örnek : (+5) + (-7) matematik cümlesini pullarla modelleyelim.
Çözüm :
Örnek : Sayma pullarıyla modellenen işlemin matematik cümlesini bulalım.
Çözüm : İşlemin matematik cümlesi, (+4) +(-3) = +1 olur.
Sayı Doğrusunda Toplama İşlemi
Sayı doğrusunda toplama işlemi yapılırken eklenen sayı pozitif ise sayı doğrusu üzerinde sağa doğru, negatif ise sola doğru gidilir.
Örnek : (+5) + (-7) matematik cümlesinin sonucunu sayı doğrusunda bulalım.
Çözüm :
(+5) + (-7) = -2 bulunur.
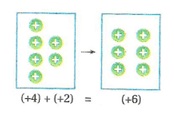
Toplanan tam sayılar pozitif ise bu sayıların mutlak değerleri toplanır ve elde edilen sonucun sonuna “+” işareti konur. Yani pozitif tam sayıların toplamının sonucu pozitiftir.
Örnek : (+7) + (+1) + (+12) işlemini sonucu kaçtır?
Çözüm : |+7| = 7, |+1| = 1, |+12| = 12 ise
(+7) + (+1) + (+12) = 7 + 1 + 12 = +20 dir.
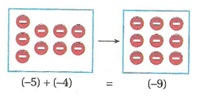
Toplanan tam sayılar negatif ise bu sayıların mutlak değerleri toplanır ve elde edilen sonucun soluna “-“ işareti konur. Yani negatif tam sayıların toplamının sonucu negatiftir.
Bir Tam Sayının Toplama İşlemine Göre Tersi
Mutlak değerleri birbirine eşit zıt işaretli iki tam sayıya toplama işlemine göre birbirinin tersi denir.
O halde pozitif tam sayıların toplama işlemine göre tersi negatif, negatif tam sayıların toplama işlemine göre tersi pozitiftir. Sıfırın toplama işlemine göre tersi sıfırdır.
Tam Sayılarda Çıkarma İşlemi
- Pullarla Çıkarma İşlemi
Olduğunu öğrenmiştir.
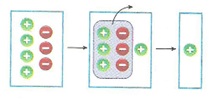
Örnek : (-5) – (-8) işleminin sonucunu sayma pullarıyla modelleyelim.
Çözüm : -5’ten -8 çıkarabilmemiz için 3 tane daha (-) pula ihtiyacımız olduğundan 3 tane sıfır çifti ekleyelim.
8 tane (-) pulu çıkardığımızda;
3 tane (+) pulu kalır.
O halde,
(-5) – (-) = +3 olur.
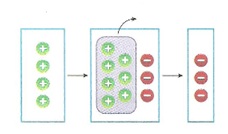
Örnek : Yukarıda sayma pullarıyla modellenen işlemin matematik cümlesini bulalım.
Çözüm : 4 tane (+) pulun yanına 3 tane sıfır çifti getirilerek 7 tane (+) pul çıkarılarak geriye 3 tane (-) pul kalmıştır.
O halde işlemin matematik cümlesi;
(+4) – (+7) = -3 olur.
- Tam sayılarla Çıkarma İşlemi
A (eksilen) – B (çıkan) = C (fark)
A + (+3) = (+7) işleminde
A tam sayısı,
A = (+7) – (+3)
A = +4 olarak bulunur.
A ve b birer tam sayı olmak üzere,
(+a) – (+b) = (+a) + (-b)
(+a) – (-b) = (+a) + (+b)olur.
Örnek : (+42) – (+27) = (+42) + (-27) = +15
Örnek : (+12) – (-5) = (+12) + (+5) = +17
Örnek : (-20) – (-8) = (-20) + (+8) = -12
Örnek : (-6) – (+4) = (-6) + (-4) = -10
Tam Sayılarda Çarpma Bölme Konu Anlatımı
Tam Sayılar çarpılırken önce işaretler çarpılır, sonra sayıların mutlak değeri çarpılır.
Aynı işaretli iki sayının çarpımı (+)
Ters işaretli iki sayının çarpımı (-) dir.
Çarpma işlemi “x” işareti ile gösterildiği gibi “.” işareti ile de gösterilir.
Örnek : (+5) . (+4) = +20
Örnek : (-5) . (-4) = +20
Örnek : (+5) . (-4) = -20
Örnek : (-4) . (+5) = -20
Çarpma İşleminin Özellikleri
- Kapalılık Özelliği
İki tam sayının çarpımı yine bir tam sayıdır. Tam sayılar kümesi çarpma işlemine göre kapalıdır.
Örnek : (-2) ∈ Z ve (+3) ∈ Z iken (-2).(+3) = (-6) ∈ Z dir.
- Değişme Özelliği
İki tam sayı çarpılırken çarpanların yerleri değiştirilirse, çarpım değişmez.
Örnek : (+3).(-4) = (-4).(+3)
(-12) = (-12) değişme özelliği vardır.
- Birleşme Özelliği
Tam sayılar kümesinde çarpma işleminin birleşme özelliği vardır. Bu nedenle ikiden fazla tam sayı birbiri ile çarpılırken çarpma işlemine istediğimiz sayıdan başlayabiliriz. Çarpım değişmez.
Örnek : [(-3).(+2)](-5) = (-3).[(+2).(-5)]
(-6).(-5) = (-3).(-10)
(+30) = (+30) dur.
Birleşme özelliği vardır.
- Etkisiz Eleman
(+1) çarpma işleminin etkisiz (birim) elemanıdır. Bu nedenle bir tam sayı (+1) ile çarpıldığında, sonuç aynı tam sayıdır.
A ∈ Z iken a.(+1) = (+1).a = a dır.
Örnek : (-5).(+1) = (-5) tir.
- Yutan Eleman
Sıfırın herhangi bir sayı ile çarpımı sıfırdır. Sıfır, çarpma işlemine göre yutan elemandır.
A ∈ Z iken a.0 = 0.a = 0 dır.
Örnek : (-5).0 = 0 dır.
- Ters Eleman
İki sayının çarpımı, çarpmanın etkisiz elemanı (+1) i veriyorsa, bu iki sayı çarpma işlemine göre birbirinin tersidir.
(+1)(+1) = (+1) dir.
(-1)(-1) = (+1) dir.
(+1) ve (-1) in dışında diğer tam sayıların çarpma işlemine göre ters elemanı yoktur.
- Çarpmanın Toplama ve Çıkarma Üzerine Dağılma Özelliği
A ∈ Z, b ∈ Z, c ∈ Z ise ,
a . (b+c) = (a.b) + (a.c) dir.
- (b-c) = (a.b) – (a.c) dir.
Örnek :
(+2). [(-3) + (-4)] = [(+2).(-3)] + [(+2).(-4)]
(+2).(-7) = (-6) + (-8)
(-14) = (-14) tür.
Bölme İşlemi
Tam sayılar bölünürken, önce işaretler bölünür. Daha sonra sayıların mutlak değerleri bölünür. Aynı işaretli iki sayının bölümü pozitif, farklı işaretli iki sayının bölümü negatiftir.
Örnek : (+15) : (+3) = (+5) ya da (+15) / (+3) = (+5)
Örnek : (-24) : (-8) = (+3) ya da (-24) / (-8) = (+3)
Bölme İşleminin Özellikleri
Tam sayılar kümesinde bölme işleminin kapalılık, değişme, birleşme özellikleri ile etkisiz elemanı yoktur.
Bir tam sayının 1 e bölümü, sayının kendisine eşittir.
A : (+1) = a
Örnek : (-8) : (+1) = (-8) dir.
Sıfırın, sıfırdan farklı bir tam sayıya bölümü sıfırdır.
0/3 = 0 0:8 = 0
Sıfırdan farklı bir sayının sıfıra bölümü tanımsızdır.
A : 0 = a/0 = Tanımsız
Pozitif iki sayı arasında bölme işlemi yapılırken, parantez olmadan da bölme işlemi yapılabilr.
(+4) : ( +2) = 4 : 2 gibi.
Negatif sayılar paranteze alınarak yazılmalıdır.
(-4) : (-2) gibi
| 7. Sınıf Matematik | Açıklama | Test Linki |
| 2. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Çözümlü Sorular | Teste Başla |
| 3. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Testleri | Teste Başla |
| 4. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Test | Teste Başla |
| 5. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Testi | Teste Başla |
| 6. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Online Test | Teste Başla |
| 7. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Test Çöz | Teste Başla |
| 8. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Problemleri | Teste Başla |
| 9. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Genel Değerlendirme | Teste Başla |
| 10. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 11. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 12. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 13. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 14. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 15. Tam Sayılarda Toplama | 7. Sınıf Tam Sayılarda Toplama Testleri Çöz | Teste Başla |
| 16. Tam Sayılarda Çıkarma | 7. Sınıf Tam Sayılarda Çıkarma Testleri Çöz | Teste Başla |
| 17. Tam Sayılarda Çarpma | 7. Sınıf Tam Sayılarda Çarpma Testleri Çöz | Teste Başla |
| 18. Tam Sayılarda Bölme | 7. Sınıf Tam Sayılarda Bölme Testleri Çöz | Teste Başla |
| 19. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Çözümlü Sorular | Teste Başla |
| 20. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Testleri | Teste Başla |
| 21. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Test | Teste Başla |
| 22. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Testi | Teste Başla |
| 23. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Online Test | Teste Başla |
| 24. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Testleri | Teste Başla |
| 25. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Test | Teste Başla |
| 26. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Testi | Teste Başla |
| 27. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Online Test | Teste Başla |
| 28. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Test Çöz | Teste Başla |
Kategoriler: Matematik Etiketler:
Matematik Konu Anlatımı
5. Sınıf Matematik Konu Anlatımı
6. Sınıf Matematik Konu Anlatımı
| Doğal Sayılarla İşlemler | Ondalık Gösterim | Cebirsel İfadeler |
| Üslü Nicelikler | Ondalık Gösterimleri Çözümleme | Örüntü ve İlişkiler |
| İşlem Önceliği | Ondalık Gösterimleri Yuvarlama | Alan Ölçme |
| Doğal Sayıların Çarpanları ve Katları | Ondalık Gösterimlerle Toplama Çıkarma | Paralelkenarın Alanı |
| Bölünebilme Kuralları | Ondalık Gösterimlerle Çarpma Bölme | Üçgenin Alanı |
| Asal Sayılar | Veri Toplama ve Düzenleme | Arazi Ölçme Birimleri |
| Açılar | Aritmetik Ortalama ve Açıklık | Prizmaların Hacmi |
| Oran Orantı | Tam Sayılar | Hacim Ölçme Birimleri |
| Toplama Çıkarma | Mutlak Değer | Prizmaların Hacmini Hesaplama |
| Çarpma Bölme | Tam Sayılarla Toplama ve Çıkarma | Sıvıları Ölçme |
7. Sınıf Matematik Konu Anlatımı
8. Sınıf Matematik Konu Anlatımı
Kategoriler: Matematik, Matematik, Matematik, Matematik Etiketler: 5 matematik konu anlatımı, 6 matematik konu anlatımı, 7 matematik konu anlatımı, 8 matematik konu anlatımı
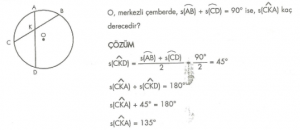
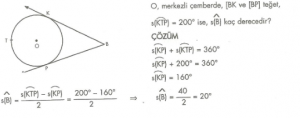
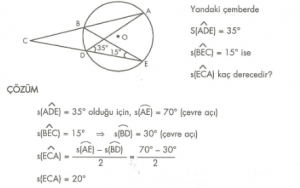
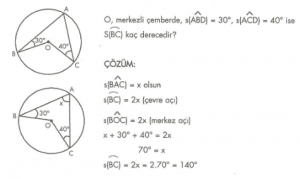
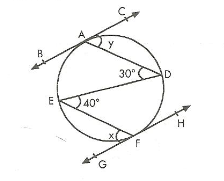
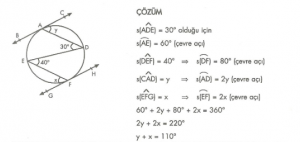
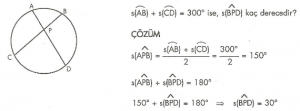
7. Sınıf Matematik Çember ve Dairede Açılar Çözümlü Sorular
7. Sınıf Matematik Çember ve Dairede Açılar Çözümlü Sorular
| 7. Sınıf Çember ve Dairede Açılar | Açıklama | Online Test Linkleri |
| Çember ve Dairede Açılar (1) | 7. Sınıf Matematik Çember ve Dairede Açılar Testleri | Teste Başla |
| Çember ve Dairede Açılar (2) | 7. Sınıf Matematik Çember ve Dairede Açılar Test | Teste Başla |
| Çember ve Dairede Açılar (3) | 7. Sınıf Matematik Çember ve Dairede Açılar Testi | Teste Başla |
| Çember ve Dairede Açılar (4) | 7. Sınıf Matematik Çember ve Dairede Açılar Online Test | Teste Başla |
| Çember ve Dairede Açılar (5) | 7. Sınıf Matematik Çember ve Dairede Açılar Test Çöz | Teste Başla |
| Çember ve Dairede Açılar (6) | 7. Sınıf Matematik Çember ve Dairede Açılar Problemleri | Teste Başla |
| Çember ve Dairede Açılar (7) | 7. Sınıf Matematik Çember ve Dairede Açılar Soruları | Teste Başla |
| Çember ve Dairede Açılar (8) | 7. Sınıf Matematik Çember ve Dairede Açılar İle İlgili Sorular | Teste Başla |
| Çember ve Dairede Açılar (9) | 7. Sınıf Matematik Çember ve Dairede Açılar İle İlgili Test Çöz | Teste Başla |
| Çember ve Dairede Açılar (10) | 7. Sınıf Matematik Çember ve Dairede Açılar Test Çöz | Teste Başla |
| Çember ve Dairede Açılar (11) | 7. Sınıf Çember ve Dairede Açılar Soru Çöz | Teste Başla |
| Çember ve Dairede Açılar (12) | 7. Sınıf Çember ve Dairede Açılar Genel Değerlendirme | Teste Başla |
7. Sınıf Matematik Çember ve Daire Çözümlü Sorular
7. Sınıf Matematik Çember ve Daire Çözümlü Sorular
| 7. Sınıf Çember ve Daire | Açıklama | Online Test Linkleri |
| Çember ve Daire (1) | 7. Sınıf Matematik Çember ve Daire Testleri | Teste Başla |
| Çember ve Daire (2) | 7. Sınıf Matematik Çember ve Daire Test | Teste Başla |
| Çember ve Daire (3) | 7. Sınıf Matematik Çember ve Daire Testi | Teste Başla |
| Çember ve Daire (4) | 7. Sınıf Matematik Çember ve Daire Online Test | Teste Başla |
| Çember ve Daire (5) | 7. Sınıf Matematik Çember ve Daire Test Çöz | Teste Başla |
| Çember ve Daire (6) | 7. Sınıf Matematik Çember ve Daire Problemleri | Teste Başla |
| Çember ve Daire (7) | 7. Sınıf Matematik Çember ve Daire Soruları | Teste Başla |
| Çember ve Daire (8) | 7. Sınıf Matematik Çember ve Daire İle İlgili Sorular | Teste Başla |
| Çember ve Daire (9) | 7. Sınıf Matematik Çember ve Daire Genel Değerlendirme | Teste Başla |
| Çember ve Daire (10) | 7. Sınıf Matematik Çember ve Daire Konu Tarama | Teste Başla |
| Çember ve Daire (11) | 7. Sınıf Çember ve Daire Deneme Sınavı 1 | Testi Çöz |
| Çember ve Daire (12) | 7. Sınıf Çember ve Daire Deneme Sınavı 2 | Testi Çöz |
| Çember ve Daire (13) | 7. Sınıf Çember ve Daire Deneme Sınavı 3 | Testi Çöz |
| Çember ve Daire (14) | 7. Sınıf Çember ve Daire Deneme Sınavı 4 | Testi Çöz |
| Çember ve Daire (15) | 7. Sınıf Çember ve Daire Deneme Sınavı 5 | Testi Çöz |