6.Sınıf Matematik Açılar Testleri Çöz
6. sınıf matematik öğrencileri aşağıdaki geniş kapsamlı açılar testlerini çözerek okuldaki başarılarını artırabilirler. Testi bitirdiğinizde kaç doğru ve kaç yanlış yaptığınızı kontrol edebilirsiniz. Sınava başlamak için aşağıdaki “Başla” butonuna tıklayabilirsiniz.
6. sınıf açılar testleri her sene yeni eğitim sistemine göre güncellenmektedir. Sınavdan önce buradaki testleri çözerek okuldaki başarınızı artırabilirsiniz. En geniş kapsamlı açılar testlerini sitemizden çözebilirsiniz.
Toplamda 16 test ve 166 adet açılar sorusu ve konu anlatımı bulunmaktadır. Sıkılmadan çözebilesiniz diye testleri 10’ar soruluk hazırladık. Bugünkü eğitim sisteminde sınavların önemi tartışılmaz. Bu zorlu yarışta ne kadar çok test çözerseniz o kadar başarılı olursunuz. Tüm öğrencilerimize başarılar dileriz!
6. Sınıf Matematik Açılar
# 6. Sınıf Matematik Açılar Konu Anlatımı
# 6. Sınıf Matematik Açılar 1
# 6. Sınıf Matematik Açılar 2
# 6. Sınıf Matematik Açılar 3
# 6. Sınıf Matematik Açılar 4
# 6. Sınıf Matematik Açılar 5
# 6. Sınıf Matematik Açılar 6
# 6. Sınıf Matematik Açılar 7
# 6. Sınıf Matematik Açılar 8
# 6. Sınıf Matematik Açılar 9
# 6. Sınıf Matematik Açılar 10
# 6. Sınıf Matematik Açılar ve Çokgenler 11
# 6. Sınıf Matematik Açılar ve Çokgenler 12
# 6. Sınıf Matematik Açılar ve Çokgenler 13
# 6. Sınıf Matematik Açılar ve Çokgenler 14
# 6. Sınıf Matematik Açılar ve Çokgenler 15
# 6. Sınıf Matematik Açılar ve Çokgenler 16
Açılar Konu Anlatımı
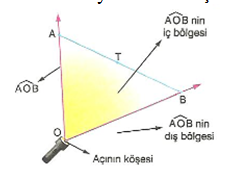
Aşağıdaki ışık kaynağı fenerden çıkan [OA ve [OB ışınlarının başlangıç noktaları ortaktır. [OA ve [OB ışınlarının arasında kalan bölgeyi tarayalım. AOB açısı oluşur. Başlangıç noktaları aynı olan iki ışın açı oluşturur.
A ve B noktalarını birleştirip üzerinde T noktası belirleyelim. A ve B noktaları hariç, [AB] üzerinde bulunan tüm noktalar açının iç bölgesi üzerindedir. T noktası açının iç bölgesidir.
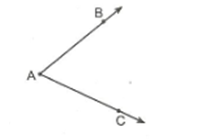
Başlangıç noktaları aynı olan iki ışının birleşimiyle oluşan şekle açı denir.
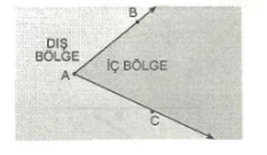
A açısı, BAC açısı veya CAB açısı diye isimlendirilir, Â, BÂC veya CÂB olarak gösterilir. [AB ve [AC ışınları açısının kendisini, ışınların içinde kalan bölge açısının iç bölgesini, ışınlarının dışında kalan bölge ise açının dış bölgesini oluşturur.
BÂC ile BÂC’nın iç bölgesinin birleşimine açısal bölge denir ve (BÂC) biçiminde gösterilir. Kağıt, üzerinde alınan bir noktadan iki farklı doğrultuda katlanırsa iç bölge ve dış bölge gözlemlenebilir.
ÇOK KOLAY KİM HAZIRLADIYSA ELLERİNE SAĞLIK
1000000000000000
teşekkurler
testler süper hazırlayan abilerim ablarım çok sağolun
yapılmayo