7. Sınıf Matematik Faktöriyel ve Permütasyon Konu Anlatımı
Faktöriyel ve Permütasyon
4 kişinin katıldığı bir yarışmada sıralamanın kaç farklı şekilde gerçekleşebileceğini bulunuz.
Bu yarışta birinci 4 yarışmacıdan biri olabilir, ikinci geri kalan 4 – 1 = 3 kişiden biri, üçüncü de geri kalan 3 – 1 = 2 kişiden biri ve dördüncü geri kalan yarışmacıdır.
Bu sıralamanın sayısı;
4.3.2.1 = 24 değişik şekilde gerçekleşebilir.
Not : 1’den n’e kadar (veya n’den geriye doğru 1’e kadar) olan doğal sayıların çarpımı “n! (n faktöriyel)” biçiminde gösterilebilir.
n! = 1.2.3 … (n-1) . n’dir.
n! = n.(n-1) … 3.2.1’dir.
0! = 1 kabul edilir.
n! = n.(n-1) …. 2.1 şeklinde yazılarak hesaplanabilir.
8 kişilik bir grup sporcu arasından 5 kişilik basketbol ekibi kaç farklı şekilde sıralanabilirler?
Bu takım için ilk kişi 8 farklı şekilde, bunu izleyen diğer dört kişi de 7,6,5,4 farklı şekilde seçilebilir. Bu sıralama 8.7.6.5.4 = 6720 farklı şekilde gerçekleşebilir.
Bu hesaplamayı faktöriyel kullanarak tekrar ifade edersek;
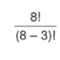 ifadesi 8’in 5’li permütasyonu olarak adlandırılır ve P(8,5 şeklinde gösterilir.
ifadesi 8’in 5’li permütasyonu olarak adlandırılır ve P(8,5 şeklinde gösterilir.
Not : n ve r birer doğal sayı, r≤n olmak üzere n’nin r’li permütasyonlarının (dizilişlerinin) sayısı P(n,r) şeklinde gösterilir.
Örnek : Okul korosu bir törende söylemek istediği 5 şarkının sıralamasını kaç farklı şekilde yapabilir?
Çözüm : 
Örnek : {1,2,3,4} kümesinin elemanlarıyla kaç tane rakamları birbirinden farklı 3 basamaklı sayı yazılabilir?
Çözüm : P(4,3) = 4.3.2 = 24 farklı şekilde yazılabilir.

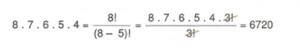
tmm bilüyoz