6. Sınıf Matematik Örüntüler ve İlişkiler Testleri Çöz
6. sınıf matematik öğrencileri aşağıdaki geniş kapsamlı örüntüler ve ilişkiler testlerini çözerek okuldaki başarılarını artırabilirler. Testi bitirdiğinizde kaç doğru ve kaç yanlış yaptığınızı kontrol edebilirsiniz. Sınava başlamak için aşağıdaki “Başla” butonuna tıklayabilirsiniz.
6. sınıf örüntüler ve ilişkiler testleri her sene yeni eğitim sistemine göre güncellenmektedir. Sınavdan önce buradaki testleri çözerek okuldaki başarınızı artırabilirsiniz. En geniş kapsamlı Örüntüler ve İlişkiler testlerini sitemizden çözebilirsiniz.
Toplamda 8 test ve yaklaşık 78 adet örüntüler ve ilişkiler sorusu ve konu anlatımı bulunmaktadır. Sıkılmadan çözebilesiniz diye testleri 10’ar soruluk hazırladık. Bugünkü eğitim sisteminde sınavların önemi tartışılmaz. Bu zorlu yarışta ne kadar çok test çözerseniz o kadar başarılı olursunuz. Tüm öğrencilerimize başarılar dileriz!
6. Sınıf Matematik Örüntüler ve İlişkiler
# Örüntüler ve İlişkiler Konu Anlatımı
# Örüntüler ve İlişkiler 1
# Örüntüler ve İlişkiler 2
# Örüntüler ve İlişkiler 3
# Örüntüler ve İlişkiler 4
# Örüntüler ve İlişkiler 5
# Örüntüler ve İlişkiler 6
# Örüntüler ve İlişkiler 7
# Örüntüler ve Denklemler 8
Örüntü ve İlişkiler Konu Anlatım
Sayıların belirli kurala göre dizilmesiyle oluşan sayı kümesine sayı örüntüsü denir.
Bir sayı örüntüsü yazalım.
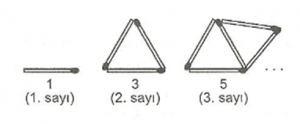
1 3 5 7 …
Bu sayı örüntüsünü üreten sayı ilişkisini bulalım.
Her kibrit çöpü 1 sayısını temsil etsin.
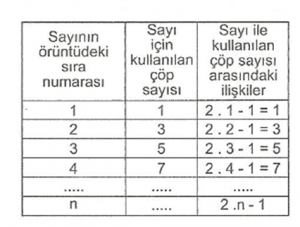
Yukarıdaki tabloyu incelersek her sayı için, sayının sıra numarasının 2 katından 1 çıkarılır. n harfi örüntüdeki sayıların sırasını belirtir. Bu yüzen n sayısına örüntünün “n. sayısı” veya “temsilci sayısı” veya “genel sayısı” denir.
n yerine herhangi bir doğal sayı konarak, sırası bu doğal sayı olan sayı bulunabilir.
Örneğin yukarıda verilen örüntünün 10. sayısını bulalım.
N = 10 için 2 . n – 1 = 2 . 10 – 1
= 20 – 1
= 19
Yani örüntüdeki 10. Sayı 19 dur.
İpucu : Sayı örüntüsündeki n harfi örüntüdeki sayıların sırasına temsil eder. Örüntünün n. sayısına örüntünün genel sayısı veya temsilci sayısı denir. Sayı örüntüsünün temsilcisindeki n yerine istenilen bir doğal sayı konulduğunda sırası bu doğal sayı olan örüntünün sayısı bulunur.
Örnek : 2 4 6 8 ….. sayı örüntüsündeki 16. sayıyı bulunuz.
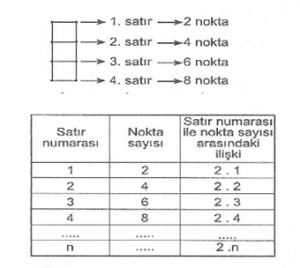
Çözüm : Örüntüdeki her sayı, sayının sırasını belirten satıra kadar olan noktaların toplamına eşittir.
Bu sayı örüntüsünün genel sayısı 2n’dir.
- sayı için n = 16 alınır.
2 . n = 2 . 16
= 32
Örüntüdeki 16. sayı 32’dir.
Örnek : 100.000 sayısı 10 sayısının kaçıncı kuvvetidir?
a) 3 b) 4 c) 5 d) 6
Çözüm : 100.000 = 10 X 10 X 10 X 10 X 10 = 105 dir.
Ayrıca 100.000 sayısında 5 tane 0 olduğundan 105 olarak yazılabilir. Tabanı 10, kuvveti 5’tir.
Doğru yanıt “C” seçeneğidir.
Benzer Testler
- 6. Sınıf Matematik Örüntüler ve İlişkiler Konu Anlatımı
- Matematik Konu Anlatımı
- 6. Sınıf Matematik Örüntüler ve İlişkiler Genel Değerlendirme
- 6. Sınıf Matematik Örüntüler ve İlişkiler Test Çöz
- 6. Sınıf Matematik Örüntüler ve İlişkiler Online Test
- 6. Sınıf Matematik Örüntüler ve İlişkiler Test
- 6. Sınıf Matematik Örüntüler ve İlişkiler Testleri
- 6. Sınıf Matematik Testleri