7. Sınıf Matematik Tam Sayılar Konu Anlatımı
Tam Sayılar
Günlük yaşantımızda bazı kavramları ifade etmek için doğal sayılar yeterli değildir.
Sıfırdan küçük sayılara da ihtiyaç vardır.
Mesela aşağıdaki termometreleri inceleyelim.
- termometrede sıcaklık sıfırın altında 10 C (ya da – 10 C)
- termometrede sıcaklık sıfırın üstünde 20 C (ya da – 20 C) dir.
Sıfırın altındaki sıcaklıkların önüne (-), sıfırın üstündeki sıcaklıkların önüne (+) işareti konulur.
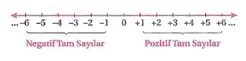
Sıfırdan büyük olan tam sayılara pozitif tam sayılar denir ve Z+ ile gösterilir.
Z+ = {+1, +2, +3, ……}
Sıfırdan küçük olan tam sayılara negatif tam sayılar denir ve Z– ile gösterilir.
Z– = {…….., -3, -2, -1}
Not : Tam sayılara aynı zamanda yönlü sayılar da denir. Bir yön pozitif (+) olduğunda, bu yönün tersi negatif (-) olur.
Örnek – 1
Bir ailenin aylık geliri 1000 TL -> +1000 TL
Bir ailenin aylık gideri 700 TL -> -700 TL
Bir malın satışından elde edilen
80 TL kar -> +80 TL
Bir malın satışından edilen
35 TL zarar -> -35 TL
Deniz seviyesinin 40 m altı -> -40m
Deniz seviyesinin 20 m üstü +20m
Not : Sıfırın işareti yoktur. Yani “0” ne negatif ne de pozitiftir.
O halde tam sayıları tanımlayacak olursak;
Negatif tam sayılar, “0” ve pozitif tam sayıların oluşturduğu kümeye tam sayılar kümesi denir ve Z ile gösterilir.
Z = Z– ∪ {0} ∪ Z+
Z 0 {…, -3, -2, -1, 0, 1, 2, 3, …}
Her tam sayıya, sayı doğrusu üzerinde bir nokta karşılık gelir ve bu noktaya o tam sayının görüntüsü denir.
Sıfır sayısının görüntüsü olan “0” noktası da başlangıç veya referans noktası denir.
Tam Sayılarda Toplama Çıkarma Konu Anlatımı
Tam Sayılarda Toplama İşlemi
- Pullarla Toplama İşlemi
Örnek : Erzurum’da hava sıcaklığı +4 C dir.
Erzurum’da hava sıcaklığı 2 C artarsa sıcaklığın kaç derece olduğunu bulalım.
Çözüm :
Erzurum’da hava sıcaklığı +6 C olur.
Örnek : Ardahan’da hava sıcaklığı -5 C dir.
Hava sıcaklığı 4 C azalırsa son durumda Ardahan’da sıcaklığın kaç derece olacağını bulalım.
Çözüm :
Ardahan’da hava sıcaklığı -9 C olur.
Örnek : (+5) + (-7) matematik cümlesini pullarla modelleyelim.
Çözüm :
Örnek : Sayma pullarıyla modellenen işlemin matematik cümlesini bulalım.
Çözüm : İşlemin matematik cümlesi, (+4) +(-3) = +1 olur.
Sayı Doğrusunda Toplama İşlemi
Sayı doğrusunda toplama işlemi yapılırken eklenen sayı pozitif ise sayı doğrusu üzerinde sağa doğru, negatif ise sola doğru gidilir.
Örnek : (+5) + (-7) matematik cümlesinin sonucunu sayı doğrusunda bulalım.
Çözüm :
(+5) + (-7) = -2 bulunur.
Toplanan tam sayılar pozitif ise bu sayıların mutlak değerleri toplanır ve elde edilen sonucun sonuna “+” işareti konur. Yani pozitif tam sayıların toplamının sonucu pozitiftir.
Örnek : (+7) + (+1) + (+12) işlemini sonucu kaçtır?
Çözüm : |+7| = 7, |+1| = 1, |+12| = 12 ise
(+7) + (+1) + (+12) = 7 + 1 + 12 = +20 dir.
Toplanan tam sayılar negatif ise bu sayıların mutlak değerleri toplanır ve elde edilen sonucun soluna “-“ işareti konur. Yani negatif tam sayıların toplamının sonucu negatiftir.
Bir Tam Sayının Toplama İşlemine Göre Tersi
Mutlak değerleri birbirine eşit zıt işaretli iki tam sayıya toplama işlemine göre birbirinin tersi denir.
O halde pozitif tam sayıların toplama işlemine göre tersi negatif, negatif tam sayıların toplama işlemine göre tersi pozitiftir. Sıfırın toplama işlemine göre tersi sıfırdır.
Tam Sayılarda Çıkarma İşlemi
- Pullarla Çıkarma İşlemi
Olduğunu öğrenmiştir.
Örnek : (-5) – (-8) işleminin sonucunu sayma pullarıyla modelleyelim.
Çözüm : -5’ten -8 çıkarabilmemiz için 3 tane daha (-) pula ihtiyacımız olduğundan 3 tane sıfır çifti ekleyelim.
8 tane (-) pulu çıkardığımızda;
3 tane (+) pulu kalır.
O halde,
(-5) – (-) = +3 olur.
Örnek : Yukarıda sayma pullarıyla modellenen işlemin matematik cümlesini bulalım.
Çözüm : 4 tane (+) pulun yanına 3 tane sıfır çifti getirilerek 7 tane (+) pul çıkarılarak geriye 3 tane (-) pul kalmıştır.
O halde işlemin matematik cümlesi;
(+4) – (+7) = -3 olur.
- Tam sayılarla Çıkarma İşlemi
A (eksilen) – B (çıkan) = C (fark)
A + (+3) = (+7) işleminde
A tam sayısı,
A = (+7) – (+3)
A = +4 olarak bulunur.
A ve b birer tam sayı olmak üzere,
(+a) – (+b) = (+a) + (-b)
(+a) – (-b) = (+a) + (+b)olur.
Örnek : (+42) – (+27) = (+42) + (-27) = +15
Örnek : (+12) – (-5) = (+12) + (+5) = +17
Örnek : (-20) – (-8) = (-20) + (+8) = -12
Örnek : (-6) – (+4) = (-6) + (-4) = -10
Tam Sayılarda Çarpma Bölme Konu Anlatımı
Tam Sayılar çarpılırken önce işaretler çarpılır, sonra sayıların mutlak değeri çarpılır.
Aynı işaretli iki sayının çarpımı (+)
Ters işaretli iki sayının çarpımı (-) dir.
Çarpma işlemi “x” işareti ile gösterildiği gibi “.” işareti ile de gösterilir.
Örnek : (+5) . (+4) = +20
Örnek : (-5) . (-4) = +20
Örnek : (+5) . (-4) = -20
Örnek : (-4) . (+5) = -20
Çarpma İşleminin Özellikleri
- Kapalılık Özelliği
İki tam sayının çarpımı yine bir tam sayıdır. Tam sayılar kümesi çarpma işlemine göre kapalıdır.
Örnek : (-2) ∈ Z ve (+3) ∈ Z iken (-2).(+3) = (-6) ∈ Z dir.
- Değişme Özelliği
İki tam sayı çarpılırken çarpanların yerleri değiştirilirse, çarpım değişmez.
Örnek : (+3).(-4) = (-4).(+3)
(-12) = (-12) değişme özelliği vardır.
- Birleşme Özelliği
Tam sayılar kümesinde çarpma işleminin birleşme özelliği vardır. Bu nedenle ikiden fazla tam sayı birbiri ile çarpılırken çarpma işlemine istediğimiz sayıdan başlayabiliriz. Çarpım değişmez.
Örnek : [(-3).(+2)](-5) = (-3).[(+2).(-5)]
(-6).(-5) = (-3).(-10)
(+30) = (+30) dur.
Birleşme özelliği vardır.
- Etkisiz Eleman
(+1) çarpma işleminin etkisiz (birim) elemanıdır. Bu nedenle bir tam sayı (+1) ile çarpıldığında, sonuç aynı tam sayıdır.
A ∈ Z iken a.(+1) = (+1).a = a dır.
Örnek : (-5).(+1) = (-5) tir.
- Yutan Eleman
Sıfırın herhangi bir sayı ile çarpımı sıfırdır. Sıfır, çarpma işlemine göre yutan elemandır.
A ∈ Z iken a.0 = 0.a = 0 dır.
Örnek : (-5).0 = 0 dır.
- Ters Eleman
İki sayının çarpımı, çarpmanın etkisiz elemanı (+1) i veriyorsa, bu iki sayı çarpma işlemine göre birbirinin tersidir.
(+1)(+1) = (+1) dir.
(-1)(-1) = (+1) dir.
(+1) ve (-1) in dışında diğer tam sayıların çarpma işlemine göre ters elemanı yoktur.
- Çarpmanın Toplama ve Çıkarma Üzerine Dağılma Özelliği
A ∈ Z, b ∈ Z, c ∈ Z ise ,
a . (b+c) = (a.b) + (a.c) dir.
- (b-c) = (a.b) – (a.c) dir.
Örnek :
(+2). [(-3) + (-4)] = [(+2).(-3)] + [(+2).(-4)]
(+2).(-7) = (-6) + (-8)
(-14) = (-14) tür.
Bölme İşlemi
Tam sayılar bölünürken, önce işaretler bölünür. Daha sonra sayıların mutlak değerleri bölünür. Aynı işaretli iki sayının bölümü pozitif, farklı işaretli iki sayının bölümü negatiftir.
Örnek : (+15) : (+3) = (+5) ya da (+15) / (+3) = (+5)
Örnek : (-24) : (-8) = (+3) ya da (-24) / (-8) = (+3)
Bölme İşleminin Özellikleri
Tam sayılar kümesinde bölme işleminin kapalılık, değişme, birleşme özellikleri ile etkisiz elemanı yoktur.
Bir tam sayının 1 e bölümü, sayının kendisine eşittir.
A : (+1) = a
Örnek : (-8) : (+1) = (-8) dir.
Sıfırın, sıfırdan farklı bir tam sayıya bölümü sıfırdır.
0/3 = 0 0:8 = 0
Sıfırdan farklı bir sayının sıfıra bölümü tanımsızdır.
A : 0 = a/0 = Tanımsız
Pozitif iki sayı arasında bölme işlemi yapılırken, parantez olmadan da bölme işlemi yapılabilr.
(+4) : ( +2) = 4 : 2 gibi.
Negatif sayılar paranteze alınarak yazılmalıdır.
(-4) : (-2) gibi
| 7. Sınıf Matematik | Açıklama | Test Linki |
| 2. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Çözümlü Sorular | Teste Başla |
| 3. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Testleri | Teste Başla |
| 4. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Test | Teste Başla |
| 5. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Testi | Teste Başla |
| 6. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Online Test | Teste Başla |
| 7. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Test Çöz | Teste Başla |
| 8. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Problemleri | Teste Başla |
| 9. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Genel Değerlendirme | Teste Başla |
| 10. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 11. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 12. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 13. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 14. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 15. Tam Sayılarda Toplama | 7. Sınıf Tam Sayılarda Toplama Testleri Çöz | Teste Başla |
| 16. Tam Sayılarda Çıkarma | 7. Sınıf Tam Sayılarda Çıkarma Testleri Çöz | Teste Başla |
| 17. Tam Sayılarda Çarpma | 7. Sınıf Tam Sayılarda Çarpma Testleri Çöz | Teste Başla |
| 18. Tam Sayılarda Bölme | 7. Sınıf Tam Sayılarda Bölme Testleri Çöz | Teste Başla |
| 19. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Çözümlü Sorular | Teste Başla |
| 20. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Testleri | Teste Başla |
| 21. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Test | Teste Başla |
| 22. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Testi | Teste Başla |
| 23. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Online Test | Teste Başla |
| 24. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Testleri | Teste Başla |
| 25. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Test | Teste Başla |
| 26. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Testi | Teste Başla |
| 27. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Online Test | Teste Başla |
| 28. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Test Çöz | Teste Başla |
📌 7. Sınıf Matematik Tam Sayılar Konu Anlatımı hakkında detaylı bilgilere ve uygulamalı örneklere bu içerikte ulaşabilirsiniz.

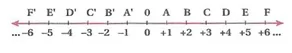

Anlamadım hiç bişiy m TŞK 😀
Benim için çok yararlı oldu teşekkürler testleri.gen.tr 🙂
?
çok güzel bir site
merhaba bana çok yardımcı oluyorsunuz şuan
çok iyi diyenler (:D ve güzel) yazsın
siteniz hata yapmış.
ilk termometre sıfırın altında 10 yani(-10)
ikinci termometre sıfırın üstünde 20 yani(+20) yerine (-20) yazılmış düzeltilmesi gerekiyor
ihbar etme yeri varsa bu yorumu kopyalayıp hata için göndersin
hata falan yapmamışlar o tire anladınmı anlamadıysan bir daha oku
aynen katılıyorum
meraba gençlik