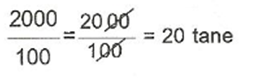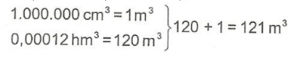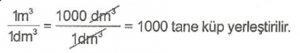6. Sınıf Matematik Kesirler Testleri Çöz
6. Sınıf Matematik Kesirler
# 6. Sınıf Matematik Kesirler 1
# 6. Sınıf Matematik Kesirler 2
# 6. Sınıf Matematik Kesirler 3
# 6. Sınıf Matematik Kesirler 4
# 6. Sınıf Matematik Kesirler 5
# 6. Sınıf Matematik Ondalık Kesirler 1
# 6. Sınıf Matematik Ondalık Kesirler 2
# 6. Sınıf Matematik Ondalık Kesirler 3
# 6. Sınıf Matematik Ondalık Kesirler 4
# 6. Sınıf Matematik Ondalık Kesirler 5
# 6. Sınıf Matematik Ondalık Kesirler 6
# 6. Sınıf Matematik Ondalık Kesirler 7
# 6. Sınıf Matematik Kesirlerle Problem
# 6. Sınıf Matematik Kesirlerde Çarpma Bölme
Kategoriler: Matematik Etiketler:
6. Sınıf Matematik Sıvıları Ölçme Konu Anlatımı
Sıvıları Ölçme
Sıvı maddeler litre ile ölçülür. Sıvı ölçüsünün temel birimi litre dir. Litre l ile gösterilir.
Sıvı ölçüsü birimleri;
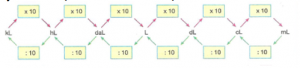
Kilolitre (kL), hektolitre (hL), dekalitre (daL), litre (L), desilitre (dL), santilitre (cL) ve mililitre (mL)’dir.
Litre :
Sıvı ölçüsü temel birimidir.
Kilolitre :
Litrenin 1000 katıdır. 1 kL = 1000 L’dir.
Hektolitre :
Litrenin 100 katıdır. 1 hL = 100 L’dir.
Dekalitre :
Litrenin 10 katıdır. 1 daL = 10 L’dir.
Desilitre :
Litrenin onda biridir. 1 dl = 1/10 L = 0,1 L’dir.
Santilitre :
Litrenin yüzde biridir. 1 cL = 1/100 L = 0,01 L’dir.
Mililitre :
Litrenin binde biridir. 1 mL = 1/1000 L = 0,001 L’dir.
Sıvı ölçüsü birimleri 10’ar 10’ar büyür, 10’ar 10’ar küçülür. Birimler arasında dönüşüm yaparken; kendisinden küçük birime çevirirken her birim için 10 ile çarpılır, kendisinden büyük birime çevirirken her birim için 10’a bölünür.
Örnek : 2 litrelik sütü kaç tane 100 mililitrelik bardağa doldurabiliriz?
a) 50 b) 40 c) 30 d) 20
Çözüm : 2 L = 2000 mL
Doğru yanıt “D” seçeneğidir.
Örnek : Şekildeki kısa kenarı 2 cm, uzun kenarı 5 cm ve yüksekliği 10 cm olan dikdörtgenler prizmasının içine en fazla kaç mL su dökebiliriz?
a) 10 b) 20 c) 50 d)100
Çözüm :
Hacim = 2 X 5 X 10 = 100 cm3
1000 cm3 = 1000 mL
olduğunu hatırlarsak 100 cm3 = 199 mL bulmuş oluruz.
Doğru yanıt “D” seçeneğidir.
Örnek : 1 hL süt 1 dm3 lük şişelere boşaltılacaktır. Bunun için kaç şişe gereklidir?
a) 100 b) 10 c) 5 d) 1
Çözüm :
1 hL = 100 L
1 L = 1 dm3 olduğundan
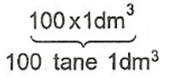
1 hL = 100 L = 100 dm3 =
Yani 100 tane 1 dm3 lük şişe gereklidir..
Doğru yanıt “A” seçeneğidir.
Örnek : Dikdörtgenler prizması şeklindeki su deposunun yüksekliği 15 cm, kısa kenarı 6 m, uzun kenarı 7 m’dir. Bu depo tamamen doldurulduğunda kaç L su alır?
- a) 42 b) 105 c) 2300 d) 630000
Çözüm :
Hacim = 15 X 6 X 7 = 630 m3
1 m3 = 630000 dm3 = 630000 L su alır.
Doğru yanıt “D” seçeneğidir.
6. Sınıf Matematik Sıvıları Ölçme
# 6. Sınıf Matematik Sıvıları Ölçme Çözümlü Sorular
# 6. Sınıf Matematik Sıvıları Ölçme Çözümlü Testler
# 6. Sınıf Matematik Sıvıları Ölçme 3
# 6. Sınıf Matematik Sıvıları Ölçme 4
# 6. Sınıf Matematik Sıvıları Ölçme 5
# 6. Sınıf Matematik Sıvıları Ölçme 6
# 6. Sınıf Matematik Sıvıları Ölçme 7
# 6. Sınıf Matematik Sıvıları Ölçme 8
# 6. Sınıf Matematik Sıvıları Ölçme 9
# 6. Sınıf Matematik Sıvıları Ölçme 10
# 6. Sınıf Matematik Sıvıları Ölçme 11
# 6. Sınıf Matematik Sıvıları Ölçme 12
# 6. Sınıf Matematik Sıvıları Ölçme 13
Kategoriler: Matematik Etiketler:
6. Sınıf Matematik Hacim Ölçme Birimleri Konu Anlatımı
Hacim Ölçme Birimleri
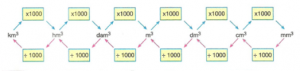
Hacim ölçme birimleri; kilometreküp (km3), hektometreküp (hm3), dekametreküp (dam3), metreküp (m3), desimetreküp (dm3), santimetreküp (cm3) ve milimetreküp (mm3)’tür.
Temel hacim ölçüsü birimi metreküp (m3)’tür.
Hacim ölçüsü birimleri 1000’er 1000’er büyür, 1000’er 1000’er küçülür. Birimler arasında dönüşüm yaparken; kendisinden küçük birime çevirmede her birim için 1000 ile çarpılır, kendisinden büyük birime çevirmede ise her birim için 1000’e bölünür.
Örnek : 0,00069 dam3 kaç dm3 tür?
a) 0,69 b) 6,9 c) 69 d) 690
Çözüm : 0,00069 dam3 = 0,69 m3 = 690 dm3 tür.
Doğru yanıt “D” seçeneğidir.
Örnek : 1.000.000 cm3 + 0,00012 hm3 kaç m3 tür?
a) 12,1 b) 22 c) 121 d) 130
Doğru yanıt “C” seçeneğidir.
Örnek : Hacmi 1 m3 olan küpün içine hacmi 1 dm3 olan küplerden kaç tane yerleştirilebilir?
a) 100 b) 1000 c) 10.000 d)100.000
Çözüm : Büyük küpün hacmini, küçük küplerin hacmine bölersek, yerleştirilebilecek küğ sayısını buluruz.
Doğru yanıt “B” seçeneğidir.
6. Sınıf Matematik Hacim Ölçme Birimleri
# 6. Sınıf Matematik Hacim Ölçme Birimleri Çözümlü Sorular
# 6. Sınıf Matematik Hacim Ölçme Birimleri 2
# 6. Sınıf Matematik Hacim Ölçme Birimleri 3
# 6. Sınıf Matematik Hacim Ölçme Birimleri 4
# 6. Sınıf Matematik Hacim Ölçme Birimleri 5
# 6. Sınıf Matematik Hacim Ölçme Birimleri 6
# 6. Sınıf Matematik Hacim Ölçme Birimleri 7
# 6. Sınıf Matematik Hacim Ölçme Birimleri 8
# 6. Sınıf Matematik Hacim Ölçme Birimleri 9
# 6. Sınıf Matematik Hacim Ölçme Birimleri 10
# 6. Sınıf Matematik Hacim Ölçme Birimleri 11
# 6. Sınıf Matematik Hacim Ölçme Birimleri 12
# 6. Sınıf Matematik Hacim Ölçme Birimleri 13
Kategoriler: Matematik Etiketler:
6. Sınıf Matematik Prizmaların Hacmi Konu Anlatımı
Prizmaların Hacmi
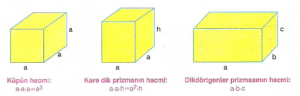
Dikdörtgenler prizmasının hacmi, tabanının uzun ve kısa kenarı ile yüksekliğinin çarpımıdır.
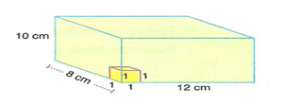
Örnek : Kenarları 1 cm olan küpler aşağıdaki dikdörtgenler prizması şeklinde kutuya doldurulacaktır. Buna göre, bu iş için kaç tane küp gerekir?
Çözüm : Önce küpün hacmi, sonra prizmanın hacmi bulunur.
Prizmanın hacmini küpün hacmine oranı gerekli küp sayısını verir.
Küpün hacmi : 1.1.1 = 1 cm3 tür.
Prizmanın hacmi : (Taban kenarlarının çarpımı) X (yükseklik)
= (8.12).10 = 960 cm3 tür. 960/1 = tane küp gerekir.
Örnek : 7 br X 10 br boyutlarındaki kareli kağıdın köşelerinden 1’er kare kesip, ayrıtlarından 1’er birim katlayarak dikdörtgenler prizması elde edelim.
Bu prizmanın hacmini hesaplayalım?
Çözüm : Elde edilen dikdörtgen prizmasının taban ayrıtları 5 br, 8 br ve yüksekliği 1 br’dir.
Hacmi : 5.8.1 = 40 br3 tür.
6. Sınıf Matematik Prizmaların Hacmi
# 6. Sınıf Matematik Prizmaların Hacmi 1
# 6. Sınıf Matematik Prizmaların Hacmi 2
Kategoriler: Matematik Etiketler:
6. Sınıf Matematik Arazi Ölçme Birimleri Konu Anlatımı
Arazi Ölçme Birimleri
Ar, dekar ve hektar arazi ölçüsü birimleridir. Bağ, bahçe ve tarla gibi arazilerin yüzeylerini ölçmede bu birimler kullanılır.
Arazi ölçüsünün temel birimi ar dır ve a ile gösterilir. 1 a = 100 m2 dir.
Ar’ın katları
Hektar (ha) : 1 ha = 100 a = 10 000 m2Dekar (daa) : 1 daa = 10 a = 1000 m2Dekar, dönüm olarak ta adlandırılır.
1 Dekar = 1 Dönüm = 1000 m2
1 Hektar = 10 Dekar
1 Hektar = 10 Dönüm
Örnek : 1 ha kaç dam2 dir?
a) 100 b) 1000 c) 10.000 d) 100.000
Çözüm : 1 ha = 100 a = 10.000 m2 = 100 dam2 dir.
Doğru yanıt “A” seçeneğidir.
Örnek : 1 km2 kaç ha dır?
a) 10 b) 100 c) 1000 d) 10.000
Çözüm :
1 km2 = 1.000.000 m2 = 10.000 a = 100 ha
Doğru yanıt “B” seçeneğidir.
Örnek : 0,6 a + 0,34 da kaç m2 dir?
a) 40 b) 346 c) 400 d) 634
Çözüm : 0,6 a = 60 m2
0,34 da = 3,4 a = 340 m2
340 + 60 = 400 m2
Doğru yanıt “C” seçeneğidir.
6. Sınıf Matematik Arazi Ölçme Birimleri
# 6. Sınıf Matematik Arazi Ölçme Birimleri 1
# 6. Sınıf Matematik Arazi Ölçme Birimleri 2
Kategoriler: Matematik Etiketler:
6. Sınıf Matematik Üçgenin Alanı Konu Anlatımı
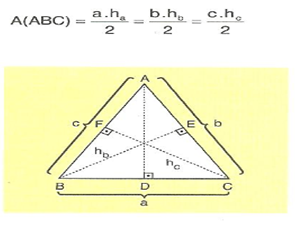
Üçgenin Alanı
Bir üçgenin alanı, bir kenar uzunluğu ile bu kenara ait yüksekliğinin çarpımının yarısına eşittir.
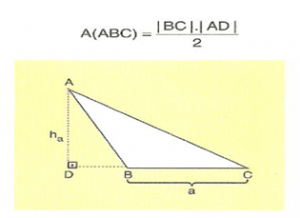
![]() ise geniş açılı ABC üçgeninde [BC]’na ait yükseklik A noktasından çizilir ve yükseklik, üçgenin dış bölgesindedir.
ise geniş açılı ABC üçgeninde [BC]’na ait yükseklik A noktasından çizilir ve yükseklik, üçgenin dış bölgesindedir.
6. Sınıf Matematik Üçgenin Alanı
# 6. Sınıf Matematik Üçgenin Alanı 1
# 6. Sınıf Matematik Üçgenin Alanı 2
Kategoriler: Matematik Etiketler:
6. Sınıf Matematik Paralelkenarın Alanı Konu Anlatımı
Paralelkenarın Özellikleri
1. Karşılıklı kenarları paraleldir. [AB] // [DC] ve [AD] // [BC]
2. Karşılıklı kenarlarının uzunlukları eşittir. |AB| = |CD| ve |AD| = |BC|
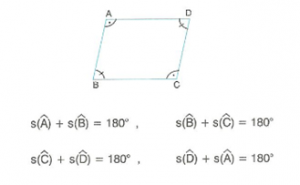
3. Karşılıklı açıların ölçüleri eşittir
4. Ardışık iki açının ölçüleri toplamı 180° dir.
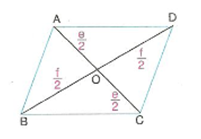
5. Köşegenler birbirini ortalar.
|AO| = |OC| = e/2 |BO| = |DO| = f/2
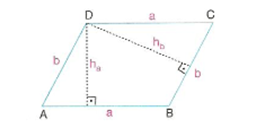
Paralelkenarın Çevresi ve Alanı
Paralelkenarın alanı, bir kenarı ile bu kenara ait yüksekliğin çarpımına eşittir. Çevresi ise 4 kenarının toplamıdır. A(ABCD) = a . ha = b . hb Ç(ABCD) = 2. (a+b) Bir köşegen paralelkenarın alanını iki eşit alana, iki köşegen dört eşit alana böler. 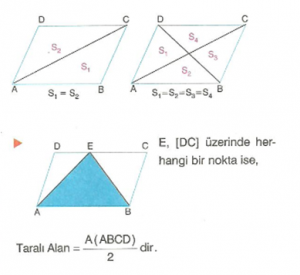
Paralelkenarın Alanı İle İlgili Online Testler
# 6. Sınıf Matematik Paralelkenarın Alanı 1 Test
# 6. Sınıf Matematik Paralelkenarın Alanı 2 Test
Kategoriler: Matematik Etiketler:
6. Sınıf Matematik Alan Ölçme Konu Anlatımı
Alan Ölçme
PASLAŞAN ALANLAR
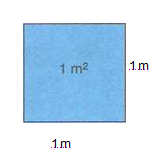
Alan ölçüsü temel birimi metrekare dir. Kenarlarının uzunluğu 1 er m olan karesel bölgenin alanına
1 metrekare denir.
Metrekare, m2 biçiminde gösterilir.
Birim kare kısaca br2 biçiminde gösterilir.
Metrekarenin Katları ve As Katları
Uzunluk birimlerinin sonuna kare sözcüğü eklenirse,
Metrekarenin katları ve as katları elde edilir.
Metrekarenin katları
Metrekarenin 100 katı olan alana dekametrekare denir.
Dekametrekare (dam2) ile gösterilir.
1 dam2 = 100 m2
Metrekarenin 10 000 katı olan alana hektometrece e denir. Hektometrekare (hm2) ile gösterilir.
1 hm2 = 10 000 m2
Metrekarenin 1000 000 katı olan alana kilometrekare denir. Kilometrekare (km2) ile gösterilir.
1 km2 = 1000 000 m2
Metrekarenin as katları
Metrekarenin 100 de biri olan alana desimetrekare denir.
Desimetrekare (dm2) ile gösterilir.
1 m2 = 100 dm2
Metrekarenin 10 000 de biri olan alana santimetrekare denir.
Santimetrekare (cm2) ile gösterilir.
1 m2 = 10 000 cm
Metrekarenin 1 000 000 da biri olan alana milimetrekare denir.
Milimetrekare (mm2) ile gösterilir.
1 m2 = 1000 000 mm2
6. Sınıf Matematik Alan Ölçme
# 6. Sınıf Matematik Alan Ölçme Çözümlü Sorular
# 6. Sınıf Matematik Alan Ölçme 2
# 6. Sınıf Matematik Alan Ölçme 3
# 6. Sınıf Matematik Alan Ölçme 4
# 6. Sınıf Matematik Alan Ölçme 5
# 6. Sınıf Matematik Alan Ölçme 6
# 6. Sınıf Matematik Alan Ölçme 7
# 6. Sınıf Matematik Alan Ölçme 8
# 6. Sınıf Matematik Alan Ölçme 9
# 6. Sınıf Matematik Alan Ölçme 10
# 6. Sınıf Matematik Alan Ölçme 11
# 6. Sınıf Matematik Alan Ölçme 12
# 6. Sınıf Matematik Alan Ölçme 13
# 6. Sınıf Matematik Alan Ölçme 14
# 6. Sınıf Matematik Alan Ölçme 15
# 6. Sınıf Matematik Alan Ölçme 16
Kategoriler: Matematik Etiketler:
6. Sınıf Matematik Örüntüler ve İlişkiler Konu Anlatımı
Örüntü ve İlişkiler
Sayıların belirli kurala göre dizilmesiyle oluşan sayı kümesine sayı örüntüsü denir.
Bir sayı örüntüsü yazalım.
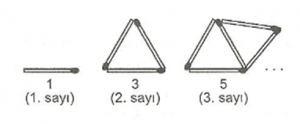
1 3 5 7 …
Bu sayı örüntüsünü üreten sayı ilişkisini bulalım.
Her kibrit çöpü 1 sayısını temsil etsin.
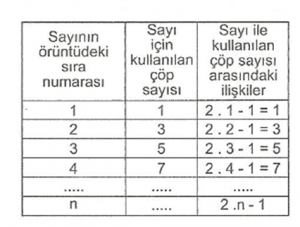
Yukarıdaki tabloyu incelersek her sayı için, sayının sıra numarasının 2 katından 1 çıkarılır. n harfi örüntüdeki sayıların sırasını belirtir. Bu yüzen n sayısına örüntünün “n. sayısı” veya “temsilci sayısı” veya “genel sayısı” denir.
n yerine herhangi bir doğal sayı konarak, sırası bu doğal sayı olan sayı bulunabilir.
Örneğin yukarıda verilen örüntünün 10. sayısını bulalım.
N = 10 için 2 . n – 1 = 2 . 10 – 1
= 20 – 1
= 19
Yani örüntüdeki 10. Sayı 19 dur.
İpucu : Sayı örüntüsündeki n harfi örüntüdeki sayıların sırasına temsil eder. Örüntünün n. sayısına örüntünün genel sayısı veya temsilci sayısı denir. Sayı örüntüsünün temsilcisindeki n yerine istenilen bir doğal sayı konulduğunda sırası bu doğal sayı olan örüntünün sayısı bulunur.
Örnek : 2 4 6 8 ….. sayı örüntüsündeki 16. sayıyı bulunuz.
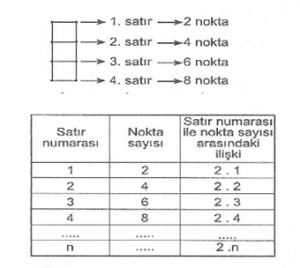
Çözüm : Örüntüdeki her sayı, sayının sırasını belirten satıra kadar olan noktaların toplamına eşittir.
Bu sayı örüntüsünün genel sayısı 2n’dir.
- sayı için n = 16 alınır.
2 . n = 2 . 16
= 32
Örüntüdeki 16. sayı 32’dir.
Örnek : 100.000 sayısı 10 sayısının kaçıncı kuvvetidir?
a) 3 b) 4 c) 5 d) 6
Çözüm : 100.000 = 10 X 10 X 10 X 10 X 10 = 105 dir.
Ayrıca 100.000 sayısında 5 tane 0 olduğundan 105 olarak yazılabilir. Tabanı 10, kuvveti 5’tir.
Doğru yanıt “C” seçeneğidir.
6. Sınıf Matematik Örüntüler ve İlişkiler
# Örüntüler ve İlişkiler 1
# Örüntüler ve İlişkiler 2
# Örüntüler ve İlişkiler 3
# Örüntüler ve İlişkiler 4
# Örüntüler ve İlişkiler 5
# Örüntüler ve İlişkiler 6
# Örüntüler ve İlişkiler 7
# Örüntüler ve Denklemler 8
Kategoriler: Matematik Etiketler:
6. Sınıf Matematik Cebirsel İfadeler Konu Anlatımı
6. Sınıf Matematik Cebirsel İfadeler konu anlatımı çalış sınavda başarıyı yakala, anlatım öğrenci düzeyleri göz önünde tutularak yer almaktadır.
Cebirsel İfadeler
En az bir bilinmeyen ve işlem içeren ifadelere cebirsel ifadeler denir.
A + 3, 9 – b, 2 x + 5, x/4 … gibi
Cebirsel ifadelerde kullanılan harfler sayıları temsil eder ve bilinmeyen (değişken) olarak adlandırılır.
A + 3 cebirsel ifadesindeki bilinmeyen a’dır.
2x + 5 cebirsel ifadesindeki bilinmeyen x’tir.
Bir cebirsel ifadede bir sayı ile bir değişken birden fazla değişkenin çarpımına terim denir.
Terimlerin sayısal çarpanına ise katsayı denir.
Terimlerin sayısal çarpanına ise katsayı denir.
İpucu : Bir cebirsel ifadede bir sayı ile değişkenin çarpımına terim, terimlerinin sayısal çarpanlarına katsayı denir.
Sayı örüntülerindeki genel sayı da bir cebirsel ifadedir. n + 2, 2n – 1 … gibi.
Örnek : “Ebru’nun elmaları, Gökhan’ın elmalarından 3 fazladır.” İfadesinde Gökhan’ın elmalarına x dersek, Ebru’nun elmaları x+3 olur. Gökhan’ın elma sayısına göre, Ebru’nın elma sayısı belirlenir.
Örnek : Aşağıdaki cebirsel ifadelerin sözel açılımlarını inceleyiniz.
X – 4 : Bir sayının 4 eksiği.
A + 5 : Bir sayının 5 fazlası.
3b + 2 : Bir sayının 3 katının 2 fazlası.
y/2 : Bir sayının yarısı.
Örnek : Aşağıdaki cebirsel ifadeleri, uygun cümlelerle eşleştiriniz.
Çözüm :
X + 7 : Ceren kardeşinden 7 erik fazla yemiş.
X – 3 : Selin, Pelin’den 3 yaş küçük.
8 – a : 8 km’lik bir yolda kalan mesafe.
5b + 1 : Bir sayının 5 katının 1 fazlası.
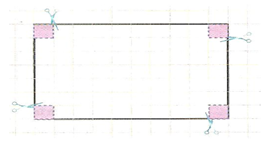
Örnek : Aşağıda bir bahçenin tepeden görünümü verilmiştir.
Aşağıda bir bahçenin tepeden görünümü verilmiştir.
a) Her duvara bir nöbetçi koymak için kaç tane nöbetçiye ihtiyaç vardır?
b) Bahçenin bir duvarının uzunluğu 3 m ise, bahçenin çevresini bulunuz.
Çözüm :
a) Bahçenin çevresi 12 tane duvardan oluştuğu için, 12 tane nöbetçi gerekir.
b) Bahçenin çevresi 12 tane duvardan oluştuğu için,
Çevre = 12x diyebilir.z
Bir duvarın uzunluğu 3m olduğundan,
Çevre 12 .3
= 36 m bulunur.
Cebirsel İfadeler Testler
# 6. Sınıf Matematik Cebirsel İfadeler Testleri Çöz
# 6. Sınıf Matematik Cebirsel İfadeler Testleri
# 6. Sınıf Matematik Cebirsel İfadeler Test
# 6. Sınıf Matematik Cebirsel İfadeler Testi
# 6. Sınıf Matematik Cebirsel İfadeler Online Test
# 6. Sınıf Matematik Cebirsel İfadeler Test Çöz
# 6. Sınıf Matematik Cebirsel İfadeler Problemleri
# 6. Sınıf Matematik Cebirsel İfadeler Soruları
# 6. Sınıf Matematik Cebirsel İfadeler Genel Değerlendirme
# 6. Sınıf Matematik Cebirsel İfadeler Konu Tarama
# 6. Sınıf Matematik Cebirsel İfadeler Deneme Sınavı
Kategoriler: Matematik Etiketler: