8. Sınıf Matematik Kareköklü Sayılarla Toplama Çıkarma Konu Anlatımı
Kareköklü Sayılarla Toplama ve Çıkarma
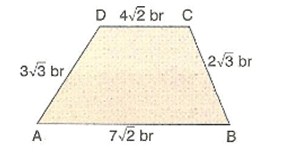
Kenar uzunlukları kareköklü sayılar olarak verilen bir yamuğun çevresi hesaplanmak istenildiğinde
ABCD yamuğunun çevresini bulmak için kenar uzunlukları toplanır.
Toplama işlemini yapmak için kök içleri aynı olan terimlerin kat sayıları toplanır.
Köklü Toplama ve Çıkarma :
Kareköklü sayılarla toplama veya çıkarma işlemini yapabilmek için, terimlerin kök içlerindeki sayılar aynı olmalıdır. Kök içlerindeki sayılar aynı olmazsa toplama veya çıkarma işlemi yapılamaz.
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Kareköklü Sayılar Konu Anlatımı
Kareköklü Sayılar
Kareköklü sayılarla matematikteki işlemler dışında birçok yerde karşılaşmaktayız. Mühendislikte formül hesaplamalarında, hassas hesaplamalarda köklü sayılarla karşılaşılır. Örneğin, bir köprünün taşıyacağı yük miktarının hesabı yapılırken sonuç köklü bir sayı çıkabilir. Alanı verilen kare şeklindeki bir bahçenin kenar uzunluğunu bulmak için karekökü bulunur. Alanı 25 m2 olan bahçenin bir kenar uzunluğu ise;
Kare şeklindeki bir havuzun alanı 16 m2 dir.
Bu havuzun bir kenar uzunluğu kaç metredir?
Kare şeklindeki alanı 16 m2 olan havuzun bir kenar uzunluğunu bulmak için karekökü bulunur.
Kendisi ile çarpıldığında 25 ve 18 olan başka sayı var mıdır?
(-5) 2 = 25
(-4) 2 = 16
Karesel Sayılar :
1, 4, 9, 16, … gibi bir doğal sayının karesi olan sayılara karesel sayılar (tam kare sayılar) denir.
Tam Kare Olmayan Sayıların Karekökleri ve İrrasyonel Sayılar
X2 = 3 eşitliğini sağlayan bir tamsayı yoktur. Fakat bu eşitliği sağlayan bir sayı vardır. Tam kare olmayan sayıların karekökleri tahmin edilirken bilinen tam kare sayıların kareköklerinden yararlanılır.
3’e en yakın tam kare sayılar 1 ve 9’dur.
Bu sayılar küçükten büyüğe doğru sıralanır.
1 < 3 < 9
Karekökleri alınır.
Sonuç 1 ile 3 arasındadır.
En yakın onda birliğe kadar sayının değerini tahmin etmek için 3’ün 1 ve 9 sayılarına olan uzaklığı düşünülür.
3 – 1 = 2 ve 9 – 3 = 6’dır.
3 sayısı 1’e 9’dan daha yakın olduğundan değeri 1,7 ile 1,8 arasındadır.
Rasyonel Olmayan Sayılar :
Ünlü Matematikçi Pisagor, dünyayı tam sayılarla ve onların birbirine oranıyla yani kesirlerle açıklayabileceğinden emindi. Ancak öğrencisi Hippasus karekök 2’nin rasyonel bir sayı olamayacağını ispatladı.
Söylenenlere göre Pisagor öğrencisi Hippasus’u öldürtmüştü.
Karekök Alma
Karekök alırken üslü sayılar ve özelliklerden yararlanılır. Karekök alma, bir sayının kök işareti içinde değerini buluğ yazmaktır. Karekökü alınacak sayının kuvveti 2’nin katı şeklinde olduğunda kök dışında rasyonel bir sayı olarak çıkar. Kuvveti 2’nin katı şeklinde olmayan sayılar kök dışına rasyonel bir sayı olarak çıkamaz.
Kökün içinde bir sayı varsa bu sayının kuvveti ikiye bölünerek kök dışında çıkar. Kökün içinde çarpım veya bölüm durumunda sayılar varsa bu sayıların kuvvetleri ayrı ayrı ikiye bölünerek kök dışına çıkar.
Çok basamaklı sayıların karekökü alınırken aşağıdaki yöntem uygulanabilir.
Sonra, 8’in karekökü bulunur. 8’in karekökü yaklaşık 2’dir. 2 = 4 sayısı 8’in altına yazılarak çıkarma işlemi yapılır.
Daha sonra, kalan 4’ün yanına 41 yazılır. Bulunan 2 sayısının 2 katı alınır. 2 x 2 = 4 sayısının sağına hangi sayı yazılıp bu sayı ile çarpılırsa 441 olacağı bulunur. Bu sayı 9’dur.
Bulunan 9 sayısı, daha önce bulunan 2’nin sağına yazılarak iki basamaklı 29 sayısı elde edilir. 841 sayısının karekökü 29’dur.
Alanı 12 m2 olan kare şeklindeki bahçenin bir kenar uzunluğu kaç metredir?
12, tam kare bir sayı değildir. 12’nin karekökü bulunurken sayı asal çarpanlara ayrılır.
| 8. Sınıf Kareköklü Sayılar | Açıklama | Test Linki |
| 1. Kareköklü Sayılar | 8. Sınıf Matematik Kareköklü Sayılar Testleri | Teste Başla |
| 2. Kareköklü Sayılar | 8. Sınıf Matematik Kareköklü Sayılar Test | Teste Başla |
| 3. Kareköklü Sayılar | 8. Sınıf Matematik Kareköklü Sayılar Testi | Teste Başla |
| 4. Kareköklü Sayılar | 8. Sınıf Matematik Kareköklü Sayılar Online Test | Teste Başla |
| 5. Kareköklü Sayılar | 8. Sınıf Matematik Kareköklü Sayılar Test Çöz | Teste Başla |
| 6. Kareköklü Sayılar | 8. Sınıf Matematik Kareköklü Sayılar Problemleri | Teste Başla |
| 7. Kareköklü Sayılar | 8. Sınıf Matematik Kareköklü Sayılar Genel Değerlendirme | Teste Başla |
| 8. Kareköklü Sayılar | 8. Sınıf Kareköklü Sayılar Konu Tarama | Teste Başla |
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Gerçek Sayılar Konu Anlatımı
Gerçek Sayılar
Matematikte şimdiye kadar kullandığımız sayıları düşünün. Bu sayıları düşünün. Bu sayıların hepsini içine alan bir sayı kümesi var mıdır? İşte bu sayı kümesi, gerçek (reel) sayılar kümesidir.
Gerçek (Reel) sayılar kümesi R ile gösterilir.
Pozitif gerçek sayılar kümesi R+, negatif gerçek sayılar kümesi R- ile gösterilir.
Reel Sayılar Kümesi :
Rasyonel sayılar kümesi ile irrasyonel sayılar kümesinin birleşim kümesidir.
Pozitif Reel Sayılar Kümesi :
0’dan büyük gerçek sayılar kümesidir.
Negatif Reel Sayılar Kümesi :
0’dan küçük gerçek sayılar kümesidir.
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Kombinasyon Konu Anlatımı
Kombinasyon
5 erkek ve 4 kızın bulunduğu bir gruptan bilgi yarışması için 3 kişi seçilecektir.
Bu seçim kaç farklı şekilde yapılabilir?
Bilgi yarışmasına katılan kişilerin hepsi kız veya hepsi erkek olabileceğinden seçim yaparken 9 kişiden 3’ünün seçileceği düşünülür.

farklı şekilde seçim yapılabilir.
Seçilen üç kişiden en az birinin kız olması, seçilen kişilerden birinin kız olması, ikisinin kız olması veya üçünün de kız olması anlamına gelir.
Toplam 3 kişi seçileceğinden
Farklı şekilde seçim yapılabilir.
Örnek : Bir düzlemde 6 nokta veriliyor.
A ) Bu noktalara kullanılarak en çok kaç doğru çizilebilir?
B ) 4’ü doğrusal ise bu noktalardan en çok kaç üçgen oluşturulabilir?
C ) Bu noktalar düzlemde en çok kaç üçgen belirtir?
| 8. Sınıf Kombinasyon | Açıklama | Test Linki |
| 1. Kombinasyon | 8. Sınıf Matematik Kombinasyon Testleri | Teste Başla |
| 2. Kombinasyon | 8. Sınıf Matematik Kombinasyon Test | Teste Başla |
| 3. Kombinasyon | 8. Sınıf Matematik Kombinasyon Testi | Teste Başla |
| 4. Kombinasyon | 8. Sınıf Matematik Kombinasyon Online Test | Teste Başla |
| 5. Kombinasyon | 8. Sınıf Matematik Kombinasyon Test Çöz | Teste Başla |
| 6. Kombinasyon | 8. Sınıf Matematik Kombinasyon Problemleri | Teste Başla |
| 7. Kombinasyon | 8. Sınıf Matematik Kombinasyon Soruları | Teste Başla |
| 8. Kombinasyon | 8. Sınıf Kombinasyon Genel Değerlendirme | Teste Başla |
| 9. Kombinasyon | 8. Sınıf Kombinasyon Konu Tarama | Teste Başla |
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Olasılık ve Olay Çeşitleri Konu Anlatımı
Olasılık ve Olay Çeşitleri
Tuttuğunuz takımın şampiyon olma olasılığı yüzde kaçtır? Favori futbolcunuzun gol kralı olma ihtimali var mıdır?
Yolda hayranı olduğunuz futbolcularla karşılaşma ihtimaliniz nedir?
Olasılık tesadüflerle yani doğruluğu kesin olmayan olaylarla ilgilenir. Olasılık hesaplarında, ortaya çıkabilecek tüm sonuçlar hesaplanır.
Zar veya madeni para gibi tahmin etme olaylarında olasılıklar hesaplanabilir.
Bir zarın havaya atılması deneydir. Zar deneyinde örnek uzay Ö = {1, 2, 3, 4, 5, 6} olduğundan s(Ö) = 6’dır.
Havaya atılan zarın üst yüzüne 1, 2, 3, 4, 5 veya 6 gelmesi ise bir olaydır.
Zarın üst yüzüne 7’den küçük bir sayma sayısının gelmesi kesin olay, 7 gelmesi imkansız olaydır.
Olasılık :
Bir olayın gerçekleşme durumunu sayısal değerlerle ifade eden matematik dalıdır.
Örnek Uzay :
Yapılan bir deneyde ortaya çıkabilecek tüm sonuçlardır. Örnek uzay “Ö” ile gösterilir.
Olay :
Örnek uzayın alt kümelerinden biridir.
Kesin Olay :
Gerçekleşmesi kesin olan olaydır. Örnek uzayın kendisine eşittir.
İmkansız Olay :
Gerçeklemesi mümkün olmayan olaydır.
Örnek : İki madeni paranın aynı anda havaya atılması deneyinde paraların ikisinin de tura gelme olayının eleman sayısı kaçtır?
Ö = {(Y,Y), (T,T), (Y,T), (T,Y)}
S(Ö) = 4’tür.
Atılan madeni paranın ikisinin de tura gelme olayına A denilirse, A = {(T,T)} olduğundan s(A) = 1’dir.
Bir Olayın Olasılığı
8 takımın katıldığı bir futbol turnuvasında her takımın diğer takımlarla bir defa maç yaptığı bilindiğine göre bu turnuvada oynanan maçların sonuçları kaç farklı şekilde gerçekleşir?
Turnuvaya 8 takım katıldığından ve her biri birbiriyle bir defa maç yaptığından turnuvada toplam 28 maç oynanır. Oynanılan bir maçta galibiyet, mağlubiyet ve beraberlik gibi 3 farklı sonuç gerçekleşebileceğinden oynanılan 28 maçın sonuçları 328 farklı şekilde gerçekleşir.
Hemen hemen hepimiz bazen ya çıkarsa diyor, büyük ikramiyeyi kazanma olasılığı düşük de olsa bir milli piyango bileti alıyor ya da sayısal loto, şans topu, on numara gibi oyunları oynuyoruz.
Sayısal lotoda büyük ikramiyenin size çıkma olasılığı nedir?
Sayısal lotoda 49 top arasından 6’sı seçilir. Seçilen 1. Topun üzerindeki sayının seçtiğimiz sayılardan biri olma olasılığı 1/49’dur.
Seçilen 6 topun üzerindeki sayıların seçtiğimiz 6 sayı olma olasılığı
Örnek : Bir çift zar aynı anda masaya atıldığında ikisinin de üst yüzüne çift sayı gelme olasılığı kaçtır?
Çift zar atıldığında s(Ö) = 62 = 36’dır. Her ikisinin de üst yüzüne çift sayı gelme olayına A denilirse
A = {(2,2), (2,4), (2,6), (4,2), (4,4), (4,6), (6,2), (6,4), (6,6)} olduğundan s(A) =9,
A Olayının Olma Olasılığı
A, örnek uzayın bir alt kümesi olmak üzere A olayının olma olasılığı
İle hesaplanır. Bu değer 0 ile 1 aralığındadır.
| 8. Sınıf Olasılık ve Olay Çeşitleri | Açıklama | Test Linki |
| 1. Olasılık ve Olay Çeşitleri | 8. Sınıf Matematik Olasılık ve Olay Çeşitleri Testleri | Teste Başla |
| 2. Olasılık ve Olay Çeşitleri | 8. Sınıf Matematik Olasılık ve Olay Çeşitleri Test | Teste Başla |
| 3. Olasılık ve Olay Çeşitleri | 8. Sınıf Matematik Olasılık ve Olay Çeşitleri Testi | Teste Başla |
| 4. Olasılık ve Olay Çeşitleri | 8. Sınıf Matematik Olasılık ve Olay Çeşitleri Online Test | Teste Başla |
| 5. Olasılık ve Olay Çeşitleri | 8. Sınıf Matematik Olasılık ve Olay Çeşitleri Test Çöz | Teste Başla |
| 6. Olasılık ve Olay Çeşitleri | 8. Sınıf Matematik Olasılık ve Olay Çeşitleri Problemleri | Teste Başla |
| 7. Olasılık ve Olay Çeşitleri | 8. Sınıf Matematik Olasılık ve Olay Çeşitleri Soruları | Teste Başla |
| 8. Olasılık ve Olay Çeşitleri | 8. Sınıf Olasılık ve Olay Çeşitleri İle İlgili Sorular | Teste Başla |
| 9. Olasılık ve Olay Çeşitleri | 8. Sınıf Olasılık ve Olay Çeşitleri İle İlgili Test Çöz | Teste Başla |
| 10. Olasılık ve Olay Çeşitleri | 8. Sınıf Olasılık ve Olay Çeşitleri Soru Çöz | Teste Başla |
| 11. Olasılık ve Olay Çeşitleri | 8. Sınıf Olasılık ve Olay Çeşitleri Genel Değerlendirme | Teste Başla |
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Tam Sayıların ve Ondalık Kesirlerin Kuvvetleri Konu Anlatımı
Tam Sayıların ve Ondalık Kesirlerin Kuvvetleri
Negatif Kuvvet
Teneffüs ettiğimiz hava, içtiğimiz su, üzerinde yürüdüğümüz yol, okuduğumuz kitap atomlardan oluşmuştur. Ellerimiz, kollarımız, ayaklarımız, beynimiz kısaca evrende görebildiğimiz ve göremediğimiz maddi olan her şeyin ana malzemesi atomdur.
Kalem ucu kadar bir noktada, yan yana dizilmiş 10 milyon tane atom yer aldığına göre, her zaman iç içe olduğumuz kendi küçük ama görevi büyük olan atomun çapı kaç milimetredir?
Etkinlik
Negatif Kuvvetler
Araç ve Gereç : İp – Makas – Cetvel
16 cm uzunluğundan bir ip parçası kesiniz.
Daha sonra bu ipi tam ortadan ikiye kesip parçalardan birini atıp diğerinin uzunluğunu aşağıdaki tabloya yazınız.
1. Elinizdeki ipi tekrar ortadan ikiye kestiğinizde yeni oluşan iplerden birinin uzunluğunun yukarıdaki tabloya yazıp diğer ipi atınız.
2. Her seferinde elinizdeki ipi tam ortadan ikiye kestiğinizde elde edilen parçalardan birinin uzunluğunun ne olduğunu hesaplayarak yukarıdaki tabloyu doldurunuz.
– 5. Kesimden sonra elde edilen küçük parçanın uzunluğunu 2 nin kuvveti olarak nasıl yazabiliriz? Tartışınız.
– 7 ve 8. Kesimlerde oluşan küçük parçalardan her birinin uzunluğunu hesaplayınız. 2’nin kuvveti olarak nasıl yazabiliriz? Tartışınız.
Bilgi Notu : Bir üslü ifade paydan paydaya ya da paydadan paya alındığında üssünün işareti değişir.
Örnek : 5’in ve 10’un kuvvetlerini bulalım.
Çözüm:
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Üslü Sayılar Konu Anlatımı
Üslü Sayılar
A bir sayı ve n bir pozitif tam sayı olmak üzere, n tane a’nın çarpımına “a’nın n. kuvveti” ya da “a üstü n” denir.
an = a.a.a.a.a…a
biçiminde gösterilir.
Sayılar yaşamın her alanındadır. Sayılarla birçok yerde karşılaşmaktayız. Çoklukların miktarı, kaç tane olduğu sayılarla ifade edilir.
Bazı çoklukların sayısı o kadar büyüktür ya da o kadar küçüktür ki yazılması güçtür.
Dünyanın en kalabalık ülkesi Çin’dir. Çin’in nüfusu yaklaşık 1.321.000.000 (1321 milyon)’dur. Okyanus sularının ağırlığı yaklaşık 1.390.000.000.000.000.000 (1390 trilyon) tondur. Virüslerin çoğunluğunun kapsit çapı 0,00001 ile 0,0003 mm arasındadır. Çok büyük ve çok küçük sayıları daha kolay ifade etmek için üslü sayılar kullanılır.
Üslü Sayıların Özellikleri
1. Bir sayının birinci kuvveti kendisine eşittir.
a1 = a
51 = 5
(-3) 1 = -3
21 = 2
2. Sıfırdan farklı bir sayının 0. kuvveti 1’e eşittir.
a0 = 1
180 = 1
(-132) 0 = 1
60 = 1
O0 = tanımsız
3. Üslü bir sayının kuvveti alınırken üsler çapımı tabana üs olarak yazılır.
(an) m = an.m
(32) 3 = 32.3 = 36
(43) 5 = 43.5 = 46
(26)7 = 26.7 = 242
Üslü Sayıların Değeri
an üslü sayısında,
a = taban
n = üs (kuvvet) tür.
24 = 2 . 2 . 2 . 2 = 16
52 = 5 . 5 = 25
Tek ve Çift Kuvvetler
Negatif bir sayının çift sayı kuvveti pozitif, tek sayı kuvveti negatiftir.
A negatif bir sayı ve n bir tam sayı olmak üzere,
a2n : pozitif
a2n+1 : negatif
(-3) 2 = (-3) . (-3) = 9
(-1) 2 = (-1) . (-1) = 1
(-6) 2 = (-6) . (-6) = 36
(-5)3 = (-5) . (-5) . (-5) = -125
Pozitif bir sayının, tek ve çift kuvvetleri pozitiftir.
a pozitif bir sayı ve n bir tam sayı olmak üzere,
a2n : pozitif
a2n+1 : pozitif
53 = 5 . 5 . 5 = 125
62 = 6 . 6 = 36
34 = 3 . 3 . 3 . 3 = 81
73 = 7 . 7 . 7 =343
Bir Sayının Pozitif ve Negatif Üssü
Bir üslü sayıda, paydan paydaya ya da paydadan paya sayıların yeri değiştirildiğinde üssün işareti değişir.
Kesirlerde Negatif Üs
Bir kesrin üssü negatif ise, kesrin payı ile paydası yer değiştirilip üssü pozitif yapılır.
a ve b birer sayı, n pozitif bir tam sayı ise,
Biliyormusunuz?
Uzun yazmak zorunda kalınan sayılar kısaca üslü sayılarla ifade edilebilirler. Örneğin 9’un 9. Kuvvetinin 9. Kuvveti, yani 9387420489 dur.Eğer bu üslü sayının değeri yazılmak istenirse 369 milyon basamağa ve 800 km uzunluğunda kağıda ihtiyaç vardır.
Örnek 1 : Karenin bir kenar uzunluğu 0,5 m’dir. Bu karenin alanı kaç santimetre karedir?
Çözüm :
A = a2
A = (0,5)2 = (0,5) . (0,5)
A = 0,25 m2
1 m2 = 10.000 cm
0,25 m2 = 2500 cm2
Üslü Sayılarda Toplam ve Fark
Üslü sayılarla toplama veya çıkarma işlemi yapabilmek için taban ve üssün aynı olması gerekir.
5.23+6.23=(5+6).23=11.23
Taban ve üssü aynı olmayan üslü sayılarla toplama veya çıkarma işlemi yapabilmek için bu üslü sayıların değeri bulunur.
23 + 52 = 2.2.2 + 5.5
8 + 25 = 33
Üslü Sayılarla Toplama ve Çıkarma
an üslü bir sayı ve x, y birer katsayı ise,
x . an + y . an = (x + y) . an
x . an – y . an = (x – y) . an
8.53+7.53=(8+7).53=15.33
9.24+8.24=(9+8).24=17.24
15.54-3.54=(15-3).54=12.54
12.62-2.62 (12-2).62=10.62
Örnek 2 : 5 + 2 . 5 – 4 . 5 işleminin sonucu kaçtır?
Çözüm : (1 + 2 – 4) . 52 = -1 . 52
= 52
Örnek 3 : 4 . 53 + 125 + 6 . 53 – 23 işleminin sonucu kaçtır?
Çözümü :
4 . 53 + 53 + 6 . 53 – 23
= (4 + 1 + 6) . 53 – 23
= 11 . 53 -23
Üslü Sayılarla Çarpma
1. Tabanları aynı, üsleri farklı üslü sayılarla çarpma
a sıfırdan farklı bir sayı ve m, n birer tam sayı ise,
am . an = am+n olur.
Tabanları aynı, üsleri farklı üslü sayılarla çarpma yaparken:
1. Taban aynen yazılır.
2. Üsler toplanıp üs olarak yazılır.
25 . 56 = 25+6 = 211
Örnek 4 : 53 . 125 . 58 . (52) 3 işleminin sonucu kaçtır?
Çözüm :
53 . 53 . 53 . 52.3
= 53 . 5 3. 58 . 56
= 53+3+8+6 = 520
2. Tabanları farklı, üsleri aynı üslü sayılarla çarpma
Tabanları farklı, üsleri aynı üslü sayılarla çarpma yaparken:
1. Tabanlar çarpılıp taban olarak yazılır.
2 Ortak üs, üs olarak yazılır.
23 . 53 = (2 . 5) 3 = 103
a ve b sıfırdan farklı birer sayı, n bir tam sayı ise,
an . bn = (a.b)n olur.
Örnek 5 : 36 . (32) 3 . 56 işleminin sonucu kaçtır?
Çözümü :
36 . 32.3 . 56
= 36 . 36 . 56
= (3 . 3 . 5) 6 = 456
3. Tabanları ve üsleri farklı üslü sayılarla çarpma
Tabanları ve üsleri farklı üslü sayılarla çarpma yaparken:
1. Üslü sayıların kuvvetleri alınarak değerleri bulunur.
2. Bulunan değerler çarpılır.
25 . 32 işleminde :
25 = 2 . 2 . 2 . 2 . 2 = 32
32 = 3 . 3 = 9
32 . 9 = 288 ‘dir.
Biliyormusunuz?
Bazı sayılar için özel eşitlikler vardır.
Sayının rakamlarının küpleri toplamı, o sayıya eşittir.
153 = 13 + 53 + 33
371 = 33 + 73 + 13
407 = 43 + 03 + 73
Benzer şekilde sayının rakamlarının 4. Kuvvetleri toplamı, o sayıya eşittir.
8208 = 84 + 24 + 04 + 84
4151 = 44 + 14 + 54 + 14
Üslü Sayılarla Bölme
1. Tabanları aynı, üsleri farklı üslü sayılarla bölme
Tabanları aynı, üsleri farklı üslü sayılarla bölme yaparken:
1. Taban aynen yazılır.
2. Üsler farkı bulunup üs olarak yazılır.
2. Tabanları farklı, üsleri aynı üslü sayılarla bölme
Tabanları farklı, üsleri aynı üslü sayılarla bölme yaparken:
1. Tabanlar bölünüp taban olarak yazılır.
2. Ortak üs, üs olarak yazılır.
Örnek 7 :
3. Tabanları ve üsleri farklı üslü sayılarla bölme
Tabanları ve üsleri farklı üslü sayılarla bölme yaparken:
1. Üslü sayıların kuvvetleri alınarak değerleri bulunur.
2. Bulunan değerler bölünür.
Örnek 8 : Dikdörtgen şeklindeki bir tarlanın alanı 5 m’dir.
Bu tarlanın kısa kenarı 5 m olduğuna göre uzun kenarı kaç metredir?
| 8. Sınıf Üslü Sayılar | Açıklama | Test Linki |
| 1. Üslü Sayılar | 8. Sınıf Matematik Üslü Sayılar Testleri | Teste Başla |
| 2. Üslü Sayılar | 8. Sınıf Matematik Üslü Sayılar Test | Teste Başla |
| 3. Üslü Sayılar | 8. Sınıf Matematik Üslü Sayılar Testi | Teste Başla |
| 4. Üslü Sayılar | 8. Sınıf Matematik Üslü Sayılar Online Test | Teste Başla |
| 5. Üslü Sayılar | 8. Sınıf Matematik Üslü Sayılar Test Çöz | Teste Başla |
| 6. Üslü Sayılar | 8. Sınıf Matematik Üslü Sayılar Problemleri | Teste Başla |
| 7. Üslü Sayılar | 8. Sınıf Matematik Üslü Sayılar Soruları | Teste Başla |
| 8. Üslü Sayılar | 8. Sınıf Üslü Sayılar İle İlgili Sorular | Teste Başla |
| 9. Üslü Sayılar | 8. Sınıf Üslü Sayılar İle İlgili Test Çöz | Teste Başla |
| 10. Üslü Sayılar | 8. Sınıf Üslü Sayılar Soru Çöz | Teste Başla |
| 11. Üslü Sayılar | 8. Sınıf Üslü Sayılar Genel Değerlendirme | Teste Başla |
| 12. Üslü Sayılar | 8. Sınıf Üslü Sayılar Konu Tarama | Teste Başla |
| 13. Üslü Sayılar | 8. Sınıf Üslü Sayılar Konu Tarama 2 | Teste Başla |
| 14. Üslü Sayılar | 8. Sınıf Üslü Sayılar Konu Tarama 3 | Teste Başla |
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Yansıma, Öteleme ve Dönme Konu Anlatımı
Yansıma, Öteleme ve Dönme
Yansıma, şeklin bir doğruya göre simetriği (ayna simetrisi)dir. Bir şeklin kendisi ile yansıması eştir. Sadece şeklin yönü terstir ve yeri değişmiştir.
Bir şeklin yansımasını bulabilmek için doğruya göre simetriği alınır. Şeklin simetriği bulunurken önce şekil üzerindeki noktalardan doğruya dikmeler inilir. Daha sonra doğrunun diğer tarafında bu noktaların doğruya eşit olan uzaklığındaki noktalar işaretlenir. Bu noktalar birleştirilerek şeklin yansıması elde edilir.
Örnek : Aşağıdaki şekilleri incelediğimizde her birinin sırasıyla 90 derece sağa döndürüldüğünü görebiliriz.
Örnek : Aşağıda, sarı renkteki şekil A noktası etrafında saat yönünde sırasıyla 90 derece döndürülmüştür.
Döndürülen şeklin biçim ve boyutu değişmez. Ancak şeklin duruşu ve yeri değişir. Bir şekil, bir nokta etrafında döndürüldüğünde o nokta dönme hareketinin merkezidir. 90 derecelik dönme çeyrek dönme, 180 derecelik dönmeye yarım dönme denir.
Bir şekil kendi merkezi etrafında 360 dereceden küçük bir açı ile döndürüldüğünde en az bir kez kendisi ile çakışıyorsa “şekil dönme simetrisine sahiptir” denir.
Örnek : Aşağıdaki şeklin bütün dönme simetri açılarını bulalım.
Çözüm : Şeklin 4 tane eş kolu olduğundan en küçük dönme simetri açısı 360:4 = 90 derecedir. Yani bu şekil en az 90 derece döndürüldüğünde kendisi ile çakışır. Diğer dönme simetri açıları ise 90 derece + 90 derece = 180 derece ve 180 derece + 90 derece = 270 derecedir.
Örnek : Aşağıda bazı sözcüklerin doğruya göre yansıması altındaki görüntüleri verilmiştir.
| 8. Sınıf Yansıma, Öteleme ve Dönme | Açıklama | Test Linki |
| 1. Yansıma, Öteleme ve Dönme | 8. Sınıf Matematik Yansıma, Öteleme ve Dönme Testleri | Teste Başla |
| 2. Yansıma, Öteleme ve Dönme | 8. Sınıf Matematik Yansıma, Öteleme ve Dönme Test | Teste Başla |
| 3. Yansıma, Öteleme ve Dönme | 8. Sınıf Matematik Yansıma, Öteleme ve Dönme Testi | Teste Başla |
| 4. Yansıma, Öteleme ve Dönme | 8. Sınıf Matematik Yansıma, Öteleme ve Dönme Online Test | Teste Başla |
| 5. Yansıma, Öteleme ve Dönme | 8. Sınıf Matematik Yansıma, Öteleme ve Dönme Test Çöz | Teste Başla |
| 6. Yansıma, Öteleme ve Dönme | 8. Sınıf Matematik Yansıma, Öteleme ve Dönme Problemleri | Teste Başla |
| 7. Yansıma, Öteleme ve Dönme | 8. Sınıf Matematik Yansıma, Öteleme ve Dönme Soruları | Teste Başla |
| 8. Yansıma, Öteleme ve Dönme | 8. Sınıf Yansıma, Öteleme ve Dönme İle İlgili Sorular | Teste Başla |
| 9. Yansıma, Öteleme ve Dönme | 8. Sınıf Yansıma, Öteleme ve Dönme Genel Değerlendirme | Teste Başla |
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Geometrik Cisimler Konu Anlatımı
Geometrik Cisimler
Dairesel Silindir :
Silindir, tabanları daire olan bir cisimdir.
Dik (Dönel) Silindir :
Bir dikdörtgenin kenarlarından biri etrafında 360 döndürülmesiyle oluşan kapalı cisimlere dik silindir denir.
Alt ve üst tabanlar r yarıçaplı eş daireler olup; tabanlar arası uzaklığa yükseklik denir ve h ile gösterilir.
Dik silindirin yan yüzü dörtgensel bölgedir. Bu dikdörtgensel bölgenin kenarlarından biri taban çevresine, diğeri ise silindirin yüksekliğine eşittir.
Eğik Silindir
Dairesel silindirin ana doğrusu tabana dik değilse, bu silindire eğik silindir denir.
|AA| = |BB| = l
Yanal ayrıtının uzunluğu l ile gösterilen eğik silindir, taban düzlemi ile a derecelik bir açı yapar.
Etkinlik
Araç Gereçler
- Kalem
- Karton Kağıt
- Pergel
- Cetvel
- Makas
Silindir Oluşturalım
Karton kağıdımıza uzun kenarı 24 cm, kısa kenarı 12 cm olacak şekilde bir dikdörtgen çizip keselim.
Oluşturduğumuz dörtgenin köşelerini isimlendirelim.
A ve B noktalarını C ile D noktalarını bir rulo oluşturacak şekilde birleştirelim.
Kartonumuzdan yarıçapı 4 cm olan iki daire çizip, keselim.
Elimizdeki daireler ile rulonun açık kalan alt ve üst tabanlarını kapatalım.
Dikdörtgenimizin kısa kenarının, oluşturduğumuz silindirin yüksekliğine; uzun kenarın ise alt ve üst tabanların oluşturan her bir dairenin çevresine eşdeğer olduğu görülür.
Çözümlü Örnekler
1. Aşağıda kapalı şekli verilen dik silindirin açık şeklini çizelim. (π = 3)
Çözüm : Taban çevresi = 2 . 3 . 5 = 30 cm
2. Şekildeki ABCD dikdörtgeninin [AB] etrafında 360 ° döndürülmesiyle oluşan cismin şeklini çizelim.
Çözüm :

3. Aşağıdakilerden hangileri silindir belirtmez?
a) Herhangi bir kenarı etrafında 360° döndürülen bir kare
b) Su bardağı
c) Herhangi bir köşesi etrafında 180° döndürülen bir kare
d) Kısa kenarı etrafında 360° döndürülen bir dikdörtgen
Çözüm :
Cevap B ve C şıklarıdır.
Not : Su bardağı üst tabanı olmayan açık bir cisimdir.
Silindir belirtmez.
4. Şekilde DEGF dikdörtgenin [DF] etrafında 180° döndürülmesiyle oluşan cismi çizelim.
Çözüm :
Şekildeki gibi bir yarım silindir oluşur.
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Eşlik ve Benzerlik Konu Anlatımı
Eşlik ve Benzerlik
Üst üste konan kağıtların hepsi birlikte kapalı düzlemsel şekil oluşturacak şekilde kesilirse bu şekillerin çakışık oldukları gözlenir ve oluşan şekiller eştir.
Üst üste çakışık durumları gözlenerek eş çokgenlerin karşılıklı kenar ve açılarının eş olduğu görülür.
Herhangi bir çokgenin kenarlarına paralel olan parçalarıyla kendine benzer bir çokgen modeli çizilebilir.
Bu modellerin birer kenarları üst üste konup kaydırılırsa kenar doğrularının da birbirine paralel olduğu fark edilir. Köşe ve kenarlar üst üste geldiğinde açıların eş, ancak kenar uzunluklarının farklı olduğu görülür. Buradan benzer çokgenlerin aynı biçimde, ancak farklı büyüklükte olduğunu söyleyebiliriz. Benzerlik için “≈” veya “∼” sembolü kullanılır.
Örnek :
Yukarıdaki şekillerden;
ABCDE beşgeni ile BCDEF beşgeni,
DEFG dörtgeni ile OPRS dörtgeni,
KLMN dörtgeni ile ABCD dörtgen kenar uzunlukları ve açıları eş olduğundan eştirler.
STUV dörtgeni ile PMNO dörtgeni,
PRSTU beşgeni ile RMNOP beşgeni,
ABC üçgeni ile DEF üçgeni açıları aynı; fakat kenar uzunlukları farklı olduğu için eş değil, benzerdirler.
Kategoriler: Matematik Etiketler: