7. Sınıf Matematik Doğrular ve Açılar Testleri Çöz
7. sınıf matematik öğrencileri aşağıdaki geniş kapsamlı doğrular ve açılar testlerini çözerek okuldaki başarılarını artırabilirler. Testi bitirdiğinizde kaç doğru ve kaç yanlış yaptığınızı kontrol edebilirsiniz. Sınava başlamak için aşağıdaki “Başla” butonuna tıklayabilirsiniz.
7. sınıf doğrular ve açılar testleri her sene yeni eğitim sistemine göre güncellenmektedir. Sınavdan önce buradaki testleri çözerek okuldaki başarınızı artırabilirsiniz. En geniş kapsamlı doğrular ve açılar testlerini sitemizden çözebilirsiniz.
Toplamda 1 tanesi çözümlü 11 test ve yaklaşık 110 adet doğrular ve açılar sorusu ve konu anlatımı bulunmaktadır. Sıkılmadan çözebilesiniz diye testleri 10’ar soruluk hazırladık. Bugünkü eğitim sisteminde sınavların önemi tartışılmaz. Bu zorlu yarışta ne kadar çok test çözerseniz o kadar başarılı olursunuz. Tüm öğrencilerimize başarılar dileriz!
7. sınıf öğrencileri matematik doğrular ve açılar ile ilgili testleri aşağıdaki linkleri kullanarak çözebilirsiniz. 7. sınıf matematik doğrular ve açılar testi çöz, 7. sınıf doğrular ve açılar testi çöz.
| 7. Sınıf Doğrular ve Açılar | Açıklama | Test Linki |
| Doğrular ve Açılar | 7. Sınıf Matematik Doğrular ve Açılar Konu Anlatımı | Konu Anlatımı |
| Doğrular ve Açılar | 7. Sınıf Matematik Doğrular ve Açılar Çözümlü Sorular | Teste Başla |
| Doğrular ve Açılar (1) | 7. Sınıf Matematik Doğrular ve Açılar Testleri | Teste Başla |
| Doğrular ve Açılar (2) | 7. Sınıf Matematik Doğrular ve Açılar Test | Teste Başla |
| Doğrular ve Açılar (3) | 7. Sınıf Matematik Doğrular ve Açılar Testi | Teste Başla |
| Doğrular ve Açılar (4) | 7. Sınıf Matematik Doğrular ve Açılar Online Test | Teste Başla |
| Doğrular ve Açılar (5) | 7. Sınıf Matematik Doğrular ve Açılar Test Çöz | Teste Başla |
| Doğrular ve Açılar (6) | 7. Sınıf Matematik Doğrular ve Açılar Soruları | Teste Başla |
| Doğrular ve Açılar (7) | 7. Sınıf Matematik Doğrular ve Açılar Genel Değerlendirme | Teste Başla |
| Doğrular ve Açılar (8) | 7. Sınıf Doğrular ve Açılar Deneme Sınavı 1 | Testi Çöz |
| Doğrular ve Açılar (9) | 7. Sınıf Doğrular ve Açılar Deneme Sınavı 2 | Testi Çöz |
| Doğrular ve Açılar (10) | 7. Sınıf Doğrular ve Açılar Deneme Sınavı 3 | Testi Çöz |
Doğrular ve Açılar Konu Anlatımı
A. Düzlemde Doğrular
1. Bir noktanın bir doğruya olan en kısa uzaklığı
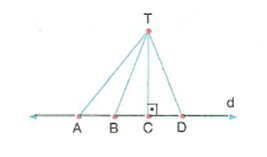
Bir noktanın bir doğruya olan en kısa uzaklığı, bu noktadan doğruya çizilen dikmenin uzunluğudur.
Yukarıdaki şekilde [TC] ⊥ d olduğundan T noktasının d doğrusuna en kısa uzaklığı |TC| dir.
2. Bir doğru parçasının orta dikmesi
Bir doğru parçasının orta dikmesi, bu doğru parçasını iki eş parçaya ayırır. Ayrıca orta dikme üzerindeki noktaların doğru parçasının uç noktalarına olan uzaklıkları birbirine eşittir.
Yukarıdaki şekilde [KC] ⊥ [AB] ve |AC| = |CB| olduğundan |TA| = |TB| ve |KA| =|KB| dir.
3. Bir Düzlemde İki Doğrunun Birbirine Göre Durumları
Çakışık Doğrular :
Aynı düzlemde ve aynı iki noktadan geçen doğrulara çakışık doğrular denir.
Kesişen Doğrular :
Aynı düzlemde yalnız bir ortak noktası bulunan doğrulara kesişen doğrular denir.
Dik Doğrular :
Aynı düzlem üzerinde bulup, birbirini dik olarak kesen doğrulardır.
Paralel Doğrular :
Aynı düzlem üzerinde bulunan ve birbirlerini hiç kesmeyen, ortak noktası bulunmayan doğrulardır.
4. Bir Düzlemde Farklı Üç Doğrunun Birbirine Göre Durumları
Bir düzlemde bulunan üç farklı doğru birbirine göre dört farklı durumda bulunurlar.
Bu durumlar,
b, d ve e doğruları bir A noktasında kesişirler.
m ile n paralel, d doğrusu ise bu iki doğruyu, farklı iki noktadan kesmektedir.
üç doğru birbirini üç farklı noktada keserler.
d, k ve n doğruları paraleldir.
B. Paralel İki Doğrunun Bir Kesenle Yaptığı Açılar
Paralel iki doğruyu üçüncü bir doğrunun kesmesiyle oluşan açılardır.
1. Yöndeş Açılar :
Paralel iki doğruyu üçüncü bir doğrunun kesmesiyle oluşan açılardan aynı yöne bakan açılara yöndeş açılar denir.
Şekilde ;
Yöndeş açıların ölçüleri birbirine eşittir.
2. İç Ters Açılar
Şekildeki
İç ters açılarının ölçüleri birbirine eşittir.
3. Dış Ters Açılar
Şekilde;
Dış ters açılarının ölçüleri birbirine eşittir.
4. Karşı Durumlu Açılar
Şekilde;
Karşı durumlu açılar bütünler açılardır.
Özel Durumlar
Şekilde; b = a+c’dir.
Şekilde görüldüğü gibi B köşesinden d ve d doğrularına paralel d doğrusu çizersek iç ters açılar oluşur. b = a + c olduğu görülür.
Paralel çizgiler arasında zikzak çizildiğinde, bir tarafa bakan açıların ölçüleri toplamı diğer tarafa bakan açıların ölçüleri toplamına eşittir.
a + b + c = x + y
[AB // [DE ise;
a + b + c = 360° dir.
[AB ve [DE ye paralel [CF çizilirse iç ters açılardan a + b + c = 360° bulunur.