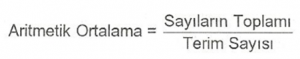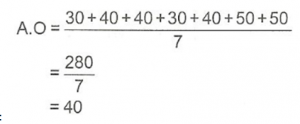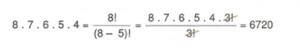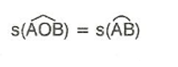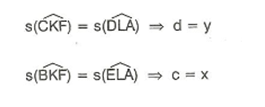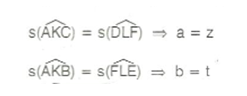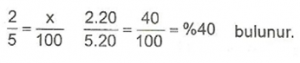7. Sınıf Matematik Tablo ve Grafikler Konu Anlatımı
Tablo ve Grafikler
Bir konu hakkında sonuç çıkarmak için gözlem ve araştırma yoluyla elde edilen bilgilerin sayılarla ifadesine istatistik denir.
İstatistik genel olarak geçmişi ve şimdiki durumu matematiksel tekniklerle analiz ederek, gelecek hakkında karar vermeyi sağlayan bir bilim dalıdır. Ancak biz, yapılan istatistik çalışmalarını doğru okumayı öğreneceğiz. Bu anlamda, rassal (rastgele) bir örneklemin, aritmetik ortalama, oran, mod, medyan gibi karakteristik değerlerini öğreneceğiz.
Örnek : Aşağıda, bir sınıfta öğrencilerin not dağılımını gösteren bir istatistik verilmiştir. 32 kişilik bir sınıfta, öğrencilerin Türkçe sınavından aldığı notlar ve öğrenci sayıları aşağıdaki gibidir.

Bilgi Toplama ve Bilgilerin Özetini Yapma
İstatistik çalışmalarının yapılabilmesi için belirlenen bir konuda doğru ve kesin bilgiler toplanır. Bilgileri toplama ve özetini yapmak için; anket yapma, rastgele seçme ve örnekleme olmak üzere üç yöntem kullanılır.
1. Anket Yapma :
Bu yöntemde, önceden hazırlanan sorular sorularak bilgi (veri) toplanır. Anket uygulaması bilimsel bir araştırmanın sadece veri toplama yöntemlerinden biridir. Daha sonra bu bilgiler yapılan araştırmalarda kullanılır.
Örnek : Piyasaya yeni çıkmış bir krem hakkında istatistik yapmak isteyen Gülşen aşağıdaki soruları hazırlamıştır.
I. Sürekli krem kullanır mısınız?
II. Bir kremde aradığınız özellikler nelerdir?
III. Bu kremi almaya nasıl karar verdiniz?
IV: Sonuçtan memnun musunuz?
Buna göre Gülşen hangi tip bilgi toplama ve özet yapma yöntemini kullanmıştır?
Genelleme
Rastgele Seçme
Anket Yapma
Örnekleme
Çözüm : Sadece anket yapma yönteminde önceden soru hazırlamak gerekir. Bu yüzden doğru cevap “Anket Yapma” olmalıdır.
Rastgele Seçme :
Örneğin bir televizyon kanalı yayınladığı programın izlenip izlenmediğini tespit etmek istediğinde bütün televizyon izleyicilerine ulaşamayacağı için, çeşitli kesimlerden rastgele seçtikleri kişilerin görüş ve isteklerine başvururlar. Bu şekilde yapılan araştırma yöntemine rastgele seçme denir?
Örnek : Çağlar yeni çıkan bir gazetenin Türkiye genelindeki günlük satış tirajına ait istatistikler oluşturmak için belli kesimlerden insanlar seçerek onların gazete hakkında fikirlerine başvuruyor. Buna göre, Çağlar hangi tip bilgi toplama ve özet yapma yöntemini kullanmıştır?
Genelleme
Rastgele Seçme
Anket Yapma
Örnekleme
Çözüm : Çağlar Türkiye genelindeki satışları tespit etmek için Türkiye’deki bütün insanlara ulaşamayacağı için belli bir kesim seçip orada araştırma yapıyor.
Örnekleme :
Örneğin bir çiftçinin yetiştirdiği zeytinin kalitesini belirlemek için kullanılır. Zeytinlerden örnekler alınarak bunların kalitesi incelenip, tüm zeytinlerin kalitesi tespit edilir. Bu yönteme örnekleme yöntemi denir?
Örnek : Sabun fabrikasında çalışan bir kimyager farklı maddelerle yapılmış sabunları inceliyor ve kalitelerine göre bir istatistik çıkarmayı planlıyor. Buna göre bu kimyager hangi tip bilgi toplama ve özet yapma yöntemini kullanmıştır?
Genelleme
Rastgele Seçme
Anket Yapma
Örnekleme
Çözüm : Farklı sabun örnekleri alınıp inceleniyor. İncelenmek üzere alınan her sabun bir “örnek” olduğuna göre “örnekleme” olmalıdır.
Örneklem : Üzerinde araştırma ve deney yapılacak gruba örneklem denir. Örneğin sivrisinek sayıları ile kurbağa sayıları arasında istatistik oluşturmak isteyen bir araştırmacının örneklem alanı bataklıklar olabilir. Çünkü sivrisinek ve kurbağa sayıları hakkındaki verilere en rahat bataklıkta ulaşılabilir.
Örnek : Özlem fast food yiyeceklerle beslenen insandaki kilo artışı üzerine bir istatistik yapmak istiyor. Bu konu hakkında anket yaparak veri toplamak isteyen Özlem’in örneklem alanı neresi olabilir?
Okullardaki 10. Sınıf öğrencileri
Oturduğu apartmandaki insanlar
Babasının iş arkadaşları
Fast food yiyeceklerin satıldığı bir yerdeki müşteriler
Çözüm : Fast food yiyeceklerle beslenen insanlara ulaşmak için en iyi yol, fast food yiyeceklerinin satıldığı yerlerdir.
Tablo Oluşturma :
Toplanan veriler, uygun bir tablo oluşturarak çetele şeklinde yazılır. Yapılan tabloya muhakkak bir başlık yazılmalıdır. Bu tabloları yorum yapmak için de kullanacağız. Daha sonra oluşturduğumuz bu tabloları grafik haline dönüştürmeyi öğreneceğiz.
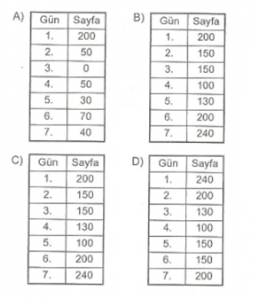
Örnek : Ebru pazartesi 200, Salı 150, Çarşamba 150, Perşembe 100, Pazar 240 sayfa kitap okuyor. Ebru’nun kitap okuma istatistiğini çıkarmak için bir tablo hazırlayan öğretmeni aşağıdaki tablolardan hangisini yapmalıdır?
Çözüm : Haftanın günleri 1, 2, 3, …….. şeklinde göstermek üzere okunan sayfa sayılarını tabloya yerleştirmeliyiz. Doğru yanıt “B” seçeneğidir.
Grafik Çeşitleri :
Verileri toplayıp özetledikten sonra bunları resim, şekil veya çizgiler yardımıyla gösteririz. Bu gösterime grafik denir. Grafikler istatistiki bilgileri anlamayı kolaylaştırır.
1. Çizgi Grafiği
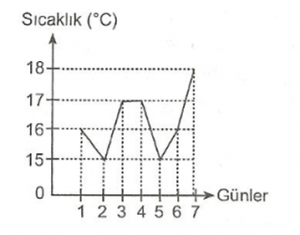
Yukarıdaki grafik, bir ilin Mayıs ayının ilk haftasına ait, sıcaklık değerlerini göstermektedir. Örneğin 5. gün sıcaklık 15 derece olur.
2. Sütun Grafiği
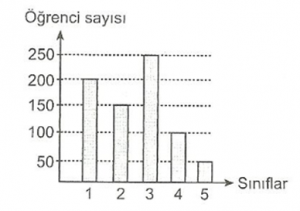
Yukarıdaki grafikte bir okulun sınıflarındaki öğrenci sayıları gösterilmiştir.
Grafiğe göre;
1. sınıfta 200 öğrenci, 2. Sınıfta 150 öğrenci, 3. Sınıfta 250 öğrenci, 4. Sınıfta 100 öğrenci ve 5. Sınıfta 50 öğrenci görmektedir.
3. Şekil Grafiği
Bir sınıftaki öğrencileri şekil grafiğiyle gösterelim.
Grafiğe göre;
Erkek öğrenci sayısı: 4 X 5 = 20 kişi
Kız öğrenci sayısı : 3 X 5 = 15
Sınıfta toplam : 20 + 15 = 35 öğrenci vardır.
Örnek :
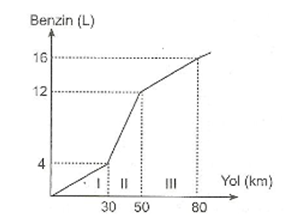
Yukarıdaki şekil bir arabanın aldığı yola göre harcadığı benzin miktarını göstermektedir. Buna göre aşağıdakilerden hangisi yanlıştır?
a) İlk 50 km’de harcanan benzin miktarı ile son 50 km’de harcanan benzin miktarı aynıdır.
b) İlk 30 km’de harcanan benzin miktarı ile son 30 km’de harcanan benzin miktarı birbirine eşittir.
c) En çok benzin III aralığında kullanılmıştır.
d) En çok benzin II aralığında kullanılmıştır.
Çözüm : Seçenekleri sırayla inceleyelim:
a) İlk 50 km’de 12 L, son 50 km’de 16 – 4 = 12 L benzin kullanılmıştır.
b) İlk 30 km’de 4 L, son 30 km’de 16 – 12 = 4L benzin kullanılmıştır.
c) I aralığında 4 L, II aralığında 12 – 4 = 8 L, III aralığında 16 – 12 = 4 L benzin kullanılmıştır. En çok benzin II aralığında kullanılmıştır.
d) En çok benzin II aralığında kullanılmıştır.
Doğru yanıt “C” seçeneğidir.
6. Sınıf Matematik Tablo ve Grafikler
# 6. Sınıf Matematik Tablo ve Grafikler 1
# 6. Sınıf Matematik Tablo ve Grafikler 2
# 6. Sınıf Matematik Tablo ve Grafikler 3
# 6. Sınıf Matematik Tablo ve Grafikler 4
# 6. Sınıf Matematik Tablo ve Grafikler 5
# 6. Sınıf Matematik Tablo ve Grafikler 6
# 6. Sınıf Matematik Tablo ve Grafikler 7
# 6. Sınıf Matematik Tablo ve Grafikler 8
# 6. Sınıf Matematik Tablo ve Grafikler 9
# 6. Sınıf Matematik Tablo ve Grafikler 10
# 6. Sınıf Matematik Tablo ve Grafikler 11
# 6. Sınıf Matematik Tablo ve Grafikler 12
# 6. Sınıf Matematik Tablo ve Grafikler 13
# 6. Sınıf Matematik Tablo ve Grafikler 14
# 6. Sınıf Matematik Tablo ve Grafikler 15
# 6. Sınıf Matematik Tablo ve Grafikler 16
# 6. Sınıf Matematik Tablo ve Grafikler 17
# 6. Sınıf Matematik Tablo ve Grafikler 18
# 6. Sınıf Matematik Tablo ve Grafikler 19
Kategoriler: Matematik Etiketler:
7.Sınıf Matematik Merkezi Eğilim ve Yayılma Ölçüleri Konu Anlatımı
Merkezi Eğilim ve Yayılma Ölçüleri
Aritmetik Ortalama :
Aritmetik orta, elimizde bulunan bütün sayıların toplamının sayı adedine bölümüdür.
Aritmetik Orta = Tüm Sayıların Toplamı/Sayı Adedi
Aralık :
Bir merkezi dağılım ölçüsüdür. Verilerin en büyük değeri ile en küçük değeri arasındaki farktır.
Aralık = En büyük değer – En küçük değer
Örnek : Bir mağazanın haftanın 7 gününe ait günlük satış 20, 18, 20, 12, 15, 17, 20 pantolondur. Buna göre bu mağazanın satış aralığı nedir?
a) 2
b) 3
c) 5
d) 8
Çözüm : Aralık = En büyük değer – En küçük değer
= 20 – 12
= 18
Doğru yanıt “D” seçeneğidir.
2. Aritmetik Ortalama :
İki veya daha fazla sayının toplanarak, terim sayısına bölünmesine aritmetik ortalama denir.
Örnek : 12, 15, 23, 98, 9, 125 sayılarının aritmetik ortalaması kaçtır?
a) 45
b) 46
c) 47
d) 48
Doğru yanıt “C” seçeneğidir.
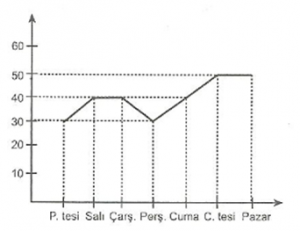
Yukarıdaki grafikte, bir öğrencinin bir hafta içinde harcadığı para miktarları gösterilmiştir. Bu öğrencilerin günlük harcadığı ortalama para miktarı kaç TL’dir.
a) 30
b) 40
c) 45
d) 50
Doğru yanıt “B” seçeneğidir.
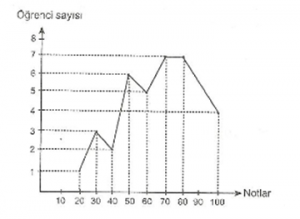
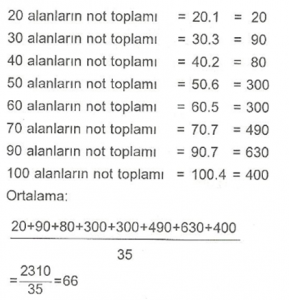
Grafikte 35 öğrencinin aldığı notlar verilmiştir. Buna göre, aşağıdakilerden hangisi doğrudur?
a) 7 öğrenci 60 almıştır.
b) En düşük ve en yüksek not alan toplam öğrenci sayısı 6’dır.
c) Sınıf mevcudu 50 alanların 7 katıdır.
d) Sınıfın not ortalaması 66’dır.
Doğru yanıt “D” seçeneğidir.
| 7. Sınıf Matematik | Açıklama | Test Linki |
| 1. Merkezi Eğilim ve Yayılma Ölçüleri | 7. Sınıf Matematik Merkezi Eğilim ve Yayılma Ölçüleri Testleri | Teste Başla |
| 2. Merkezi Eğilim ve Yayılma Ölçüleri | 7. Sınıf Matematik Merkezi Eğilim ve Yayılma Ölçüleri Online Test | Teste Başla |
| 3. Merkezi Eğilim ve Yayılma Ölçüleri | 7. Sınıf Matematik Merkezi Eğilim ve Yayılma Ölçüleri Soruları | Teste Başla |
| 4. Merkezi Eğilim ve Yayılma Ölçüleri | 7. Sınıf Matematik Merkezi Eğilim ve Yayılma Ölçüleri İle İlgili Test Çöz | Teste Başla |
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik OIasılık Konu Anlatımı
Olasılık
Olasılık İle İlgili Temel Kavramlar :
Olasılık, rastlantı ya da kesin olmayan olaylarla uğraşır. Bu sonucu kesin olmayan ya da rastlantıya bağlı olaylara “olasılık” denir.
Şans oyunları, bir zarın atılınca 4 gelmesi gibi hesaplar olasılık ile ilgilidir.
Deney :
Sonuçları belirlenebilen olaylardır. Örneğin bir paranın havaya atılması sonucunda yazı yada tura gelecektir.
Çıktılar :
Bir deneyde elde edilebilecek sonuçlara denir. Örneğin, para atma deneyinde çıktılar “yazı” ve “tura”dır.
Örnek Uzay :
Bütün çıktıların oluşturduğu kümeye denir. Ö harfi ile gösterilir.
Olay : Örnek uzayın elemanlarının birbirine denir.
Eş olasılıklı olma :
Yapılan bir deneydeki her bir çıktının olma olasılığı eşittir.
E örnek uzayında herhangi bir olay A olsun. Bu A olayının olasılığı p (A) ile gösterirsek.
Örnek 1 : İki metal para atıldığında her ikisinin yazı, birinin yazı diğerinin tura, her ikisinin tura gelme olasılığını bulalım.
Çözüm:
Deney :
İki metal paranın atılması
Örnek Uzay :
İki metal para atıldığında çıkabilecek tüm sonuçlar.
Ö = {TT, TY, YT, YY} ise s(Ö] = 4
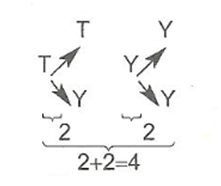
Olay :
İki metal paranın yazı gelmesi
A = {YY} ise s(A) = 1
Olayın çıktıları = YY

Olay : İki metal paranın tura gelmesi
A = {TT} ise s(A) = 1
Olayın çıktıları = TT
Olay : İki metal paradan birinin yazı diğerinin tura gelmesi
A = {YT, TY} ise s(A) = 2
Olayın çıktıları = TT.YY
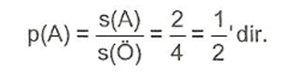
Örnek 2 : Bir torbada 1’den 6’ya kadar numaralandırılmış 6 tane top vardır. Buna göre, torbadan rastgele seçilen bir topun üzerindeki sayının çift sayı olma olasılığını bulalım.
Çözüm :
Deney :
Aynı özelliğe sahip toplar üzerine yazılmış olan 1,2,3,4,5,6 rakamlarından birinin seçilmesi
Örnek Uzay :
Bir top çekildiğinde çıkabilecek tüm sonuçlar
Ö = {1,2,3,4,5,6}, s(Ö) = 6
Olay : Çift sayı çekilmesi
A = {2, 4, 6}, s(A) = 3
Olayın çıktıları : 2, 4, 6
Eş olasılıklı olma :
Her bir sayının çekilme olasılığı eşittir.

Not : Evrensel kümede her bir eleman bir kez yazılır fakat örnek uzayda çıktılar kaç tane ise o kadar yazılır.
Örnek 3 : “KELEBEK” kelimesinin harflerinden oluşan evresel küme: E = {K, E, L, B} kümesidir. Örnek Uzay : Ö = {K, E, L, E, B, E, K} dir.
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik Faktöriyel ve Permütasyon Konu Anlatımı
Faktöriyel ve Permütasyon
4 kişinin katıldığı bir yarışmada sıralamanın kaç farklı şekilde gerçekleşebileceğini bulunuz.
Bu yarışta birinci 4 yarışmacıdan biri olabilir, ikinci geri kalan 4 – 1 = 3 kişiden biri, üçüncü de geri kalan 3 – 1 = 2 kişiden biri ve dördüncü geri kalan yarışmacıdır.
Bu sıralamanın sayısı;
4.3.2.1 = 24 değişik şekilde gerçekleşebilir.
Not : 1’den n’e kadar (veya n’den geriye doğru 1’e kadar) olan doğal sayıların çarpımı “n! (n faktöriyel)” biçiminde gösterilebilir.
n! = 1.2.3 … (n-1) . n’dir.
n! = n.(n-1) … 3.2.1’dir.
0! = 1 kabul edilir.
n! = n.(n-1) …. 2.1 şeklinde yazılarak hesaplanabilir.
8 kişilik bir grup sporcu arasından 5 kişilik basketbol ekibi kaç farklı şekilde sıralanabilirler?
Bu takım için ilk kişi 8 farklı şekilde, bunu izleyen diğer dört kişi de 7,6,5,4 farklı şekilde seçilebilir. Bu sıralama 8.7.6.5.4 = 6720 farklı şekilde gerçekleşebilir.
Bu hesaplamayı faktöriyel kullanarak tekrar ifade edersek;
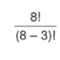 ifadesi 8’in 5’li permütasyonu olarak adlandırılır ve P(8,5 şeklinde gösterilir.
ifadesi 8’in 5’li permütasyonu olarak adlandırılır ve P(8,5 şeklinde gösterilir.
Not : n ve r birer doğal sayı, r≤n olmak üzere n’nin r’li permütasyonlarının (dizilişlerinin) sayısı P(n,r) şeklinde gösterilir.
Örnek : Okul korosu bir törende söylemek istediği 5 şarkının sıralamasını kaç farklı şekilde yapabilir?
Çözüm : 
Örnek : {1,2,3,4} kümesinin elemanlarıyla kaç tane rakamları birbirinden farklı 3 basamaklı sayı yazılabilir?
Çözüm : P(4,3) = 4.3.2 = 24 farklı şekilde yazılabilir.
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik Çember ve Dairede Açılar Konu Anlatımı
Çember ve Dairede Açılar
A. Çember
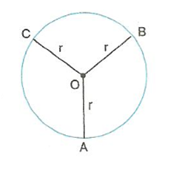
Sabit bir noktaya eşit uzaklıktaki noktalar kümesine çember denir.
Sabit nokta çemberin merkezidir. Çemberin merkezi ile çember üzerindeki noktaları birleştiren doğru parçalarına çemberin yarıçapı denir.
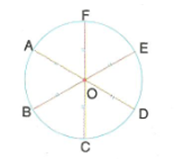
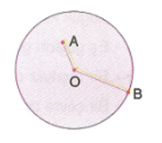
Şekilde O çemberin merkezidir.
|OA| = |OB| = |OC| = r çemberin yarıçapıdır.
Merkezi O noktası ve yarıçapı r olan çember Ç(O, r) şeklinde gösterilir.
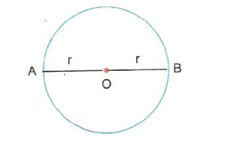
Çemberin merkezinden geçen ve |AB|= 2r uzunluğunda olan doğru parçasına çemberin çapı denir.
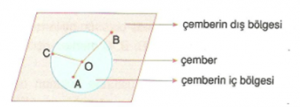
Çemberin düzlemde ayırdığı bölgeler:
Daire :
Çember ile çemberin iç bölgesinin birleşimine daire denir.
O merkezli r yarıçaplı daire D(O, r) şeklinde gösterilir.
Uyarı : Çemberin her noktası dairenin elemanıdır. Fakat dairenin iç bölgesine ait noktalar çemberin elemanı değildir. Çember ait olduğu dairenin alt kümesidir.
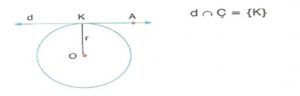
Teğet :
Çemberle bir ortak noktası olan doğruya çemberin teğeti denir.
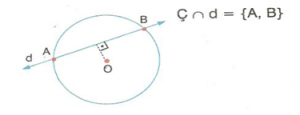
Kesen :
Bir çemberi iki noktada kesen doğruya çemberin keseni denir.
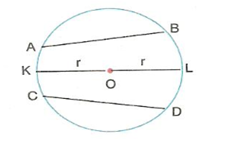
Kiriş :
Bir çemberin iki noktasını birleştiren doğru parçasına çemberin kirişi denir.
Bir çemberin merkezinden geçen kiriş, çemberin en büyük kirişidir. Bu kirişe çemberin çapı denir.
|KL| = 2|KO| = 2|OL| = 2r
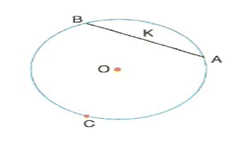
B. Çemberde Yaylar
Şekildeki çemberde verilen [AB] kirişi, çemberi iki parçaya ayırır. Bu parçalara çember yayı denir.
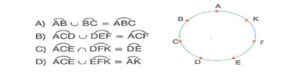
Örnek : Aşağıdaki şekilde verilen A, B, C, D, E, F ve K noktaları çemberin üzerinde ise aşağıdakilerden hangisi yanlıştır?
Çözüm : D şıkkı yanlıştır.
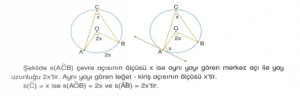
Çemberde Açılar
1. Merkez Açı :
Köşesi çemberin merkezinde olan açıya merkez açı denir.
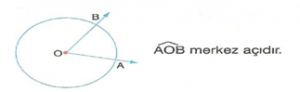
Merkez açının içinde kalan çember parçasına merkez açının gördüğü yay denir.
Merkez açının ölçüsü gördüğü yayın ölçüsüne eşittir.
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik Çember ve Daire Konu Anlatımı
Çember ve Daire
Düzlemde sabit bir noktadan eşit uzaklıkta bulunan noktaların oluşturduğu kümeye çember denir.
Sabit bir nokta (O)’dan eşit uzaklıktaki A, B, C … gibi sonsuz noktanın birleşim kümesi çemberi oluşturur. Ç (O, r) sembolü ile gösterilir.
[AB] merkezden geçip A ve B noktaları çember üzerinde bulunduğundan çap adını alır.
Çap = 2r dir.
Çap, çemberi iki eş parçaya ayırır.
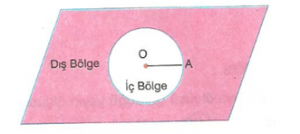
Çemberin Düzlemden Ayırdığı Bölgeler
Bir çember, içinde bulunduğu düzlemi üç ayrı noktalar kümesine ayırır.
- |OC| = r koşulunu sağlayan C noktalarının kümesi Ç(O, r) dir.
- |OA| < r koşulunu sağlayan A noktalarının kümesi, çemberin iç bölgesini oluşturur. A ∉ Ç (O, r)
- |OB| > r koşulunu sağlayan noktalar kümesi, çemberin dış bölgesini oluşturur.
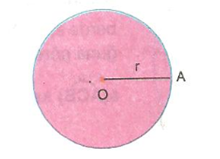
Daire
Çember ile çemberin iç bölgesinin birleşim kümesine daire çembersel bölge denir.
D (O, r) ile gösterilir.
Çember sabit bir noktadan eşit uzaklıktaki noktaların oluşturduğu kapalı bir eğridir. Daire ise çember ve çemberin iç bölgesinden oluşan bir düzlem parçasıdır.
Çemberin Elemanları ve Özellikleri
- Çemberin iki noktası arasında kalan parçasında çember yayı ya da kısaca yay denir.
- Bir çember üzerindeki iki noktadan geçen doğruya kesen denir. Kesenin çemberin içinde kalan parçasına kiriş denir.
- Merkezden geçen kirişe çap denir. Çap 2r veya R ile gösterilir.
Çemberde Açılar ve Yaylar
Merkez açısının içinde kalan çember parçasına merkez açın gördüğü yay; çevre açının içinde kalan çember parçasına da çevre açının gördüğü yay denir.
Özellikleri
- Eş kirişlerin gördüğü yayların ölçüleri eşittir.
- Büyük kirişin gördüğü yay, küçük kirişin gördüğü yaydan büyüktür.
- Eş yayları gören merkez açılar eşittir.
- Bir merkez açının ölçüsü, gördüğü yayın ölçüsüne eşittir.
- Bir çevre açının ölçüsü, aynı yayı gören merkez açının ölçüsünün yarısına eşittir.
- Bir çevre açının ölçüsü gördüğü yayın ölçüsünün yarısına eşittir. Çapı gören çevre açı 90°’dir.
- Aynı yayı gören teğet – kiriş açı ölçüsü ile çevre açı ölçüsü birbirine eşittir.
Minör ve Majör Yaylar
Minör yayların ölçüsü kendisini gören merkez açının ölçüsüne eşittir.
Majör yayın ölçüsü 360° – minör yayın ölçüsüdür.
Minör yay uzunluğu + majör yay uzunluğu = 360°’dir.
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik Dörtgenler Konu Anlatımı
Dörtgenler
Çevre uzunluları aynı olan dikdörtgenlerin alanları farklı olabilir. İlk olarak alanı büyük olan dikdörtgenin çevre uzunluğu daha büyük olmalı gibi düşünülse de durum her zaman öyle olmayabilir. Çevre uzunlukları eşit olan dikdörtgenlerden kenar uzunlukları birbirine yakın olanların alanları daha büyüktür.
Aşağıdaki örnekler incelendiğinde konu daha iyi anlaşılacaktır.
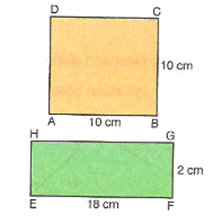
Örnek :
Yukarıdaki şekilde verilen ABCD ve EFGH dikdörtgenlerinin çevre uzunluğu ile alanlarını karşılaştırınız.
Çözüm :
Ç(ABCD) = 2(10 + 10)
= 2. 20
= 40 cm’dir.
Ç(EFGH) = 2(18 + 2)
= 2. 20
= 40 cm’dir.
A(ABCD) = 10.10
= 100 cm2
A(EFGH) = 18.2
= 36 cm2’dir.
Yukarıdaki örnekte de görüldüğü gibi ABCD dikdörtgenin çevre uzunluğu il EFGH dikdörtgenin çevre uzunluğu birbirine eşit olmasına rağmen ABCD dikdörtgenin alanı EFGH dikdörtgenin alanından büyüktür.
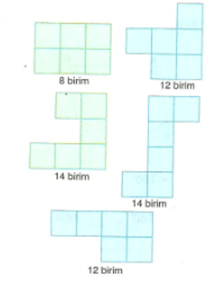
Örnek : Alanı 6 birim kare olan kareliler takımı ile elde edilebilecek şeklin çevre uzunluğu en fazla kaç birim olur?
Çözüm :
Yukarıda da görüldüğü gibi alanı 6 birim kare olan birbirinden farklı bir çok şekil çizilebilir. Çevre uzunluğu en fazla 14 birim olmaktadır.
Kareliler takımı ile oluşturulan bir şeklin alanı n birim kare ise bu şeklin olası en büyük çevre uzunluğu 2n + 2 birimdir.
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik Çokgenler Konu Anlatımı
Çokgenler
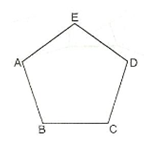
Doğrusal olmayan en az üç noktanın birleştirilmesiyle oluşan kapalı geometrik şekillere çokgen denir. Çokgenler kenar sayılarına göre isimlendirilir. N kenarlı bir çokgen “n – gen” olarak isimlendirilir. Çokgen üç kenarlı ise üçgen, dört kenarlı ise dörtgen, beş kenarlı ise beşgen, altı kenarlı ise altıgen ……. olarak isimlendirilir.
Şekildeki çokgende, A, B, C, D, E çokgenin köşeler; [AB], [BC], [CD], [DE] ve [EA] çokgenin kenarlarıdır. A, B, C, D, E köşelerine ait çokgenin iç bölgesinde kalan açılar çokgenin iç açılarını oluşturur.
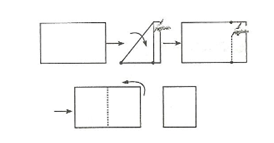
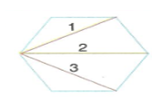
Bir kağıt kısa kenarı bir komşu uzun kenar üzerine gelecek şekilde katlanır ve uzun kenarlar üzerine gelen noktalar işaretlenir. Kağıt bu noktalardan kendi üzerine gelecek şekilde yeniden katlanırsa bir “kare” modeli oluşur.
Kağıt yardımıyla ikişer ikişer kesişen ve birbirine paralel olmayan üç kat çizgisi ile bir “üçgen” modeli oluşturulur.
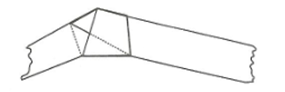
Uzun bir kağıt şerit düğüm atılarak iki ucundan çekilerek düzlenir. Yandan artan fazla parçalar kesilerek beşgen oluşturulur.
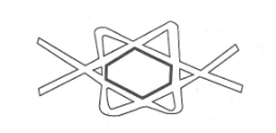
Kağıttan iki uzun şerit kesilerek şeritler şekildeki gibi katlanarak karşılıklı yerleştirilir ve iki yandan çekilerek düzlenirse fazla parçalar kesildiğinde ortada “altıgen” modeli oluşturulur.
Tüm kenar uzunlukları ve iç açılarının ölçüleri eşit olan çokgenlere düzgün çokgen denir.
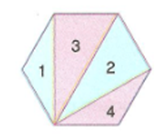
Örnek : n tane kenarı olan bir çokgenin bir köşesinden n – 3 tane köşegen çizilir.
Altıgenin bir köşesinden kaç tane köşegen çizilir?
Çözüm : n = 6 -> n – 3 = 6 – 3 = 3 tanedir.
Örnek : n tane kenarı olan bir çokgenin aynı köşesinden çizilen köşegenler n – 2 tane üçgen oluşturur.
Altıgenin bir köşesinden çizilen köşegenlere altıgenin içinde kaç tane üçgen oluştur?
Çözüm : n = 6 -> n – 2 = 6 – 2 = 4 tane üçgen oluşur.
N tane kenarı olan çokgenin iç açıları toplamı 180.(n-2)’dir.
Yedigende x ile gösterilen açının ölçüsünü bulalım.
Çözüm : n = 7 -> iç açıları toplamı 180.(7-2) = 180 . 5 = 900°
Çokgenin verilen iç açıları toplamı = 130 + 115 + 140 + 120 + 135 + 160 = 800°
Verilmeyen açı 900 – 800 = 100°’dir.
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik Doğrular ve Açılar Konu Anlatımı
Doğrular ve Açılar
A. Düzlemde Doğrular
1. Bir noktanın bir doğruya olan en kısa uzaklığı
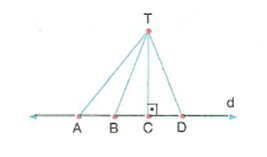
Bir noktanın bir doğruya olan en kısa uzaklığı, bu noktadan doğruya çizilen dikmenin uzunluğudur.
Yukarıdaki şekilde [TC] ⊥ d olduğundan T noktasının d doğrusuna en kısa uzaklığı |TC| dir.
2. Bir doğru parçasının orta dikmesi
Bir doğru parçasının orta dikmesi, bu doğru parçasını iki eş parçaya ayırır. Ayrıca orta dikme üzerindeki noktaların doğru parçasının uç noktalarına olan uzaklıkları birbirine eşittir.
Yukarıdaki şekilde [KC] ⊥ [AB] ve |AC| = |CB| olduğundan |TA| = |TB| ve |KA| =|KB| dir.
3. Bir Düzlemde İki Doğrunun Birbirine Göre Durumları
Çakışık Doğrular :
Aynı düzlemde ve aynı iki noktadan geçen doğrulara çakışık doğrular denir.
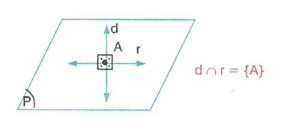
Kesişen Doğrular :
Aynı düzlemde yalnız bir ortak noktası bulunan doğrulara kesişen doğrular denir.
Dik Doğrular :
Aynı düzlem üzerinde bulup, birbirini dik olarak kesen doğrulardır.
Paralel Doğrular :
Aynı düzlem üzerinde bulunan ve birbirlerini hiç kesmeyen, ortak noktası bulunmayan doğrulardır.
4. Bir Düzlemde Farklı Üç Doğrunun Birbirine Göre Durumları
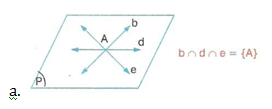
Bir düzlemde bulunan üç farklı doğru birbirine göre dört farklı durumda bulunurlar.
Bu durumlar,
b, d ve e doğruları bir A noktasında kesişirler.
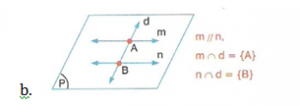
m ile n paralel, d doğrusu ise bu iki doğruyu, farklı iki noktadan kesmektedir.
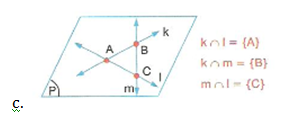
üç doğru birbirini üç farklı noktada keserler.
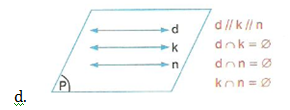
d, k ve n doğruları paraleldir.
B. Paralel İki Doğrunun Bir Kesenle Yaptığı Açılar
Paralel iki doğruyu üçüncü bir doğrunun kesmesiyle oluşan açılardır.
1. Yöndeş Açılar :
Paralel iki doğruyu üçüncü bir doğrunun kesmesiyle oluşan açılardan aynı yöne bakan açılara yöndeş açılar denir.
Şekilde ;
Yöndeş açıların ölçüleri birbirine eşittir.
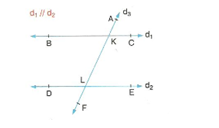
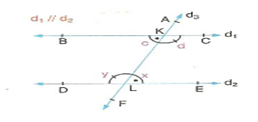
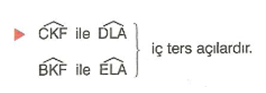
2. İç Ters Açılar
Şekildeki
İç ters açılarının ölçüleri birbirine eşittir.
3. Dış Ters Açılar
Şekilde;
Dış ters açılarının ölçüleri birbirine eşittir.
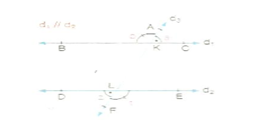
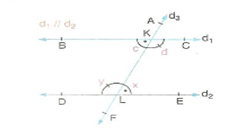
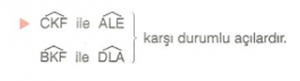
4. Karşı Durumlu Açılar
Şekilde;
Karşı durumlu açılar bütünler açılardır.
Özel Durumlar
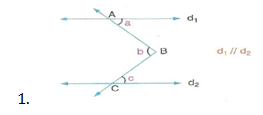
Şekilde; b = a+c’dir.
Şekilde görüldüğü gibi B köşesinden d ve d doğrularına paralel d doğrusu çizersek iç ters açılar oluşur. b = a + c olduğu görülür.
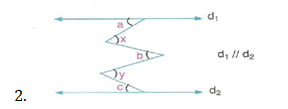
Paralel çizgiler arasında zikzak çizildiğinde, bir tarafa bakan açıların ölçüleri toplamı diğer tarafa bakan açıların ölçüleri toplamına eşittir.
a + b + c = x + y
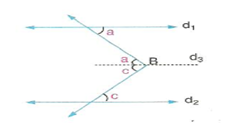
[AB // [DE ise;
a + b + c = 360° dir.
[AB ve [DE ye paralel [CF çizilirse iç ters açılardan a + b + c = 360° bulunur.
Kategoriler: Matematik Etiketler:
7.Sınıf Matematik Yüzde Hesaplamaları Konu Anlatımı
Yüzde Hesaplamaları
Ondalık Kesirleri Yüzde Sembolü İle Gösterme
Ondalık sayı önce kesir şeklinde yazılır. Paydası 100 olacak şekilde pay ve paya aynı sayma sayısı ile genişletilir. Böylece ilk kesre denk bir kesir elde edilmiş olur. Oluşan bu kesir yüzde sembolü kullanılarak yazılır.
Örnek : 2/5 kesrini yüzde sembolü ile gösterelim.
Çözüm : 2/5 kesrini yüzde sembolü ile gösterirken denk kesirlerden yararlanabiliriz.
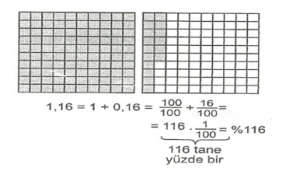
Örnek : 1,16 kesrini yüzlük kartlarla modelleyerek yüzdeye çeviriniz.
Yüzde Sembolüyle Verilen İfadenin Ondalık Kesir Şeklinde Yazılması
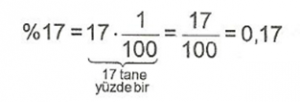
Örnek : %17 sayısının ondalık kesir olarak yazılışını bulunuz.
Sonuç olarak her yüzdelik ifade bir kesir ya da ondalık sayı olarak yazılabilir.
Not : Bir ondalık kesrin paydası 100 ise sembol ile kolayca gösterebiliriz. Ondalık kesrin paydası 100 değil ise pay ve paydası, paydası, paydayı 100 yapacak olan sayma sayısı ile çarpılır.
Eğer paydayı 100 yapacak bir sayma sayısı bulunamıyorsa pay paydaya bölünerek kesri ondalık sayı şeklinde yazmaya çalışırız.
Kesrin ondalık açılımını yazıp virgülü iki basamak sağa kaydırır ve yüzde sembolü kullanarak yazabiliriz.
Şimdi bu son durumu bir örnekle pekiştirelim.
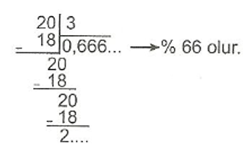
Örnek : 2/3 kesrini yüzde sembolü kullanarak gösteriniz.
Yüzde İfadelerinin Karşılaştırılması
Yüzdelik sayıları karşılaştırırken iki yöntem kullanabiliriz.
- Yüzdelik kısmı büyük olan yüzde sayısı büyüktür.
Örneğin %50 ile %55 sayısını karşılaştıralım.
Yüzdelik kısımlarına bakarsak
50 ve 55’i 50 < 55 şeklinde sıralayabiliriz.
Dolayısıyla %50 < %55 olur.
Ya da
- Yüzdelik sayıyı kesir sayısına çevirerek sıralayabiliriz.
Örneğin; %32 ile %62 yüzdelik sayılarını karşılaştıralım.
%32 = 32/100 , %62 = 62/100
Kesirler konusundan da bildiğimiz gibi paydası eşit olan iki kesrin payı küçük olan küçüktür.
Dolayısıyla 32/100 < 62/100 olur.
Yani %32 < %62 dir.
Örnek : 1,28 ve 1,39 ondalık sayılarını modelleme yöntemi ile yüzdeliğe çeviriniz ve büyüklüklerini karşılaştırınız.
139 tane yüzde bir 128 tane yüzde birden daha büyüktür. Sembolle gösterirsek %139 > %128 olur.
Örnek : %34 ile %43 yüzdeliklerini yüzlük kartlarla göstererek sıralayınız.
%34 lük ve %43 lük dilimleri farklı renklerde boyarız. Sonra bu boyalı kısımları kesip üst üste koyarak büyüklüklerini karşılaştırınız.
Yüzlük kartta görüldüğü gibi üst üste konan yüzeyler arasındaki fark farklı tonlarda boyalıdır. Böylece %34’ün %43’ten küçük olduğu şekille de gösterilmiş olur.
Kategoriler: Matematik Etiketler: