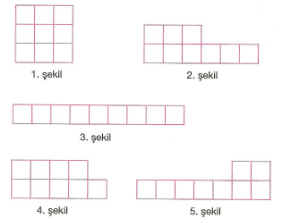
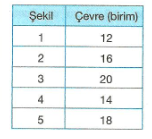
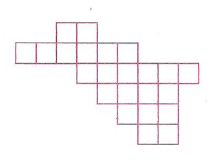
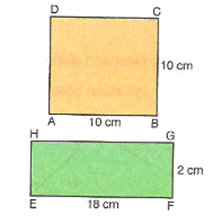
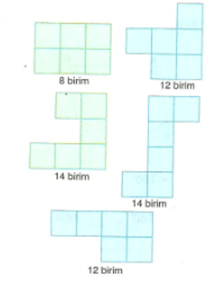
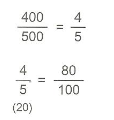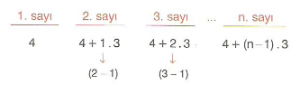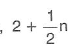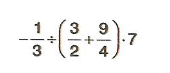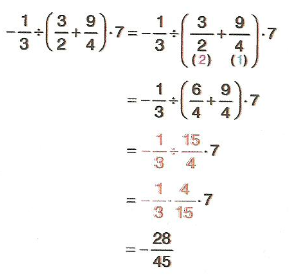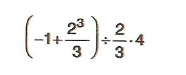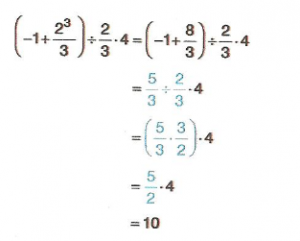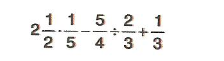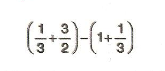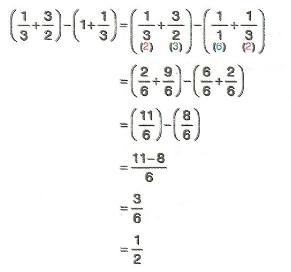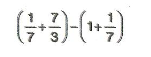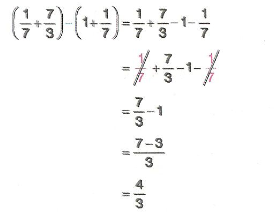7. Sınıf Matematik Dörtgenler Çözümlü Sorular
7. Sınıf Matematik Dörtgenler Çözümlü Sorular
Tebrikler - 7. Sınıf Matematik Dörtgenler Çözümlü Sorular adlı sınavı başarıyla tamamladınız.
Sizin aldığınız skor %%SCORE%% en yüksek skor %%TOTAL%%.
Hakkınızdaki düşüncemiz %%RATING%%
| 7. Sınıf Dörtgenler | Açıklama | Test Linki |
| Dörtgenler (1) | 7. Sınıf Matematik Dörtgenler Testleri | Teste Başla |
| Dörtgenler (2) | 7. Sınıf Matematik Dörtgenler Test | Teste Başla |
| Dörtgenler (3) | 7. Sınıf Matematik Dörtgenler Testi | Teste Başla |
| Dörtgenler (4) | 7. Sınıf Matematik Dörtgenler Online Test | Teste Başla |
| Dörtgenler (5) | 7. Sınıf Matematik Dörtgenler Test Çöz | Teste Başla |
| Dörtgenler (6) | 7. Sınıf Matematik Dörtgenler Problemleri | Teste Başla |
| Dörtgenler (7) | 7. Sınıf Matematik Dörtgenler Soruları | Teste Başla |
| Dörtgenler (8) | 7. Sınıf Matematik Dörtgenler İle İlgili Sorular | Teste Başla |
| Dörtgenler (9) | 7. Sınıf Matematik Dörtgenler Genel Değerlendirme | Teste Başla |
| Dörtgenler (10) | 7. Sınıf Matematik Dörtgenler Konu Tarama | Teste Başla |
| Dörtgenler (11) | 7. Sınıf Matematik Dörtgenler Deneme Sınavı | Teste Başla |
| Dörtgenler (12) | 7. Sınıf Matematik Dörtgenler Deneme Sınavı 2 | Teste Başla |
7. Sınıf Matematik Doğrular ve Açılar Çözümlü Sorular
7.Sınıf Matematik Doğrular ve Açılar Çözümlü Sorular
| 7. Sınıf Doğrular ve Açılar | Açıklama | Test Linki |
| Doğrular ve Açılar (1) | 7. Sınıf Matematik Doğrular ve Açılar Testleri | Teste Başla |
| Doğrular ve Açılar (2) | 7. Sınıf Matematik Doğrular ve Açılar Test | Teste Başla |
| Doğrular ve Açılar (3) | 7. Sınıf Matematik Doğrular ve Açılar Testi | Teste Başla |
| Doğrular ve Açılar (4) | 7. Sınıf Matematik Doğrular ve Açılar Online Test | Teste Başla |
| Doğrular ve Açılar (5) | 7. Sınıf Matematik Doğrular ve Açılar Test Çöz | Teste Başla |
| Doğrular ve Açılar (6) | 7. Sınıf Matematik Doğrular ve Açılar Soruları | Teste Başla |
| Doğrular ve Açılar (7) | 7. Sınıf Matematik Doğrular ve Açılar Genel Değerlendirme | Teste Başla |
| Doğrular ve Açılar (8) | 7. Sınıf Doğrular ve Açılar Deneme Sınavı 1 | Testi Çöz |
| Doğrular ve Açılar (9) | 7. Sınıf Doğrular ve Açılar Deneme Sınavı 2 | Testi Çöz |
| Doğrular ve Açılar (10) | 7. Sınıf Doğrular ve Açılar Deneme Sınavı 3 | Testi Çöz |
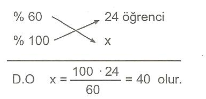
7.Sınıf Matematik Yüzde Hesaplamaları Çözümlü Sorular
7.Sınıf Matematik Yüzde Hesaplamaları Çözümlü Sorular
| 7. Sınıf Matematik | Açıklama | Test Linki |
| Yüzde Hesaplamaları (1) | 7. Sınıf Matematik Yüzde Hesaplamaları Testleri | Teste Başla |
| Yüzde Hesaplamaları (2) | 7. Sınıf Matematik Yüzde Hesaplamaları Test | Teste Başla |
| Yüzde Hesaplamaları (3) | 7. Sınıf Matematik Yüzde Hesaplamaları Testi | Teste Başla |
| Yüzde Hesaplamaları (4) | 7. Sınıf Matematik Yüzde Hesaplamaları Online Test | Teste Başla |
| Yüzde Hesaplamaları (5) | 7. Sınıf Matematik Yüzde Hesaplamaları Test Çöz | Teste Başla |
| Yüzde Hesaplamaları (6) | 7. Sınıf Matematik Yüzde Hesaplamaları Problemleri | Teste Başla |
| Yüzde Hesaplamaları (7) | 7. Sınıf Matematik Yüzde Hesaplamaları Soruları | Teste Başla |
| Yüzde Hesaplamaları (8) | 7. Sınıf Yüzde Hesaplamaları İle İlgili Sorular | Teste Başla |
| Yüzde Hesaplamaları (9) | 7. Sınıf Yüzde Hesaplamaları İle İlgili Test Çöz | Teste Başla |
| Yüzde Hesaplamaları (10) | 7. Sınıf Yüzde Hesaplamaları Testi Çöz | Teste Başla |
| Yüzde Hesaplamaları (11) | 7. Sınıf Yüzde Hesaplamaları Soru Çöz | Teste Başla |
| Yüzde Hesaplamaları (12) | 7. Sınıf Yüzde Hesaplamaları Genel Değerlendirme | Teste Başla |
| Yüzde Hesaplamaları (13) | 7. Sınıf Yüzde Hesaplamaları Deneme Sınavı | Teste Başla |
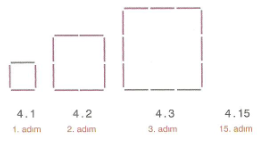
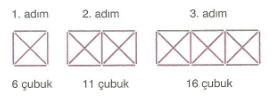
7.Sınıf Matematik Örüntüler ve İlişkiler Çözümlü Sorular
7.Sınıf Matematik Örüntüler ve İlişkiler Çözümlü Sorular
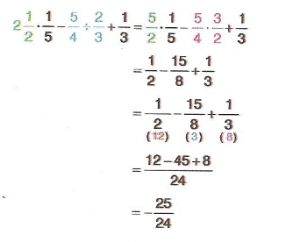
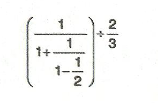
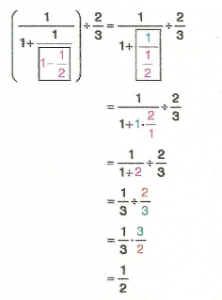
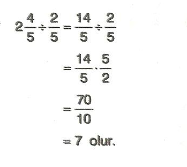
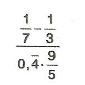
7.Sınıf Matematik Rasyonel Sayılarla Adım Adım İşlemler Çözümlü Sorular
7.Sınıf Matematik Rasyonel Sayılarla Adım Adım İşlemler Çözümlü Sorular
Kategoriler: Matematik Etiketler: 7. sınıf matematik rasyonel sayılarla adım adım işlemler çözümlü sorular, 7. sınıf matematik rasyonel sayılarla adım adım işlemler soru ve cevapları, 7. sınıf matematik rasyonel sayılarla adım adım işlemler soruları ve çözümleri, 7. sınıf matematik rasyonel sayılarla adım adım işlemler testleri ve çözümleri
7.Sınıf Matematik Tam Sayılar Çözümlü Sorular
7.Sınıf Matematik Tam Sayılar Çözümlü Sorular
| 7. Sınıf Matematik | Açıklama | Test Linki |
| 1. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Konu Anlatımı | Konu Anlatımı |
| 3. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Testleri | Teste Başla |
| 4. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Test | Teste Başla |
| 5. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Testi | Teste Başla |
| 6. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Online Test | Teste Başla |
| 7. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Test Çöz | Teste Başla |
| 8. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Problemleri | Teste Başla |
| 9. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Genel Değerlendirme | Teste Başla |
| 10. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 11. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 12. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 13. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 14. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 15. Tam Sayılarda Toplama | 7. Sınıf Tam Sayılarda Toplama Testleri Çöz | Teste Başla |
| 16. Tam Sayılarda Çıkarma | 7. Sınıf Tam Sayılarda Çıkarma Testleri Çöz | Teste Başla |
| 17. Tam Sayılarda Çarpma | 7. Sınıf Tam Sayılarda Çarpma Testleri Çöz | Teste Başla |
| 18. Tam Sayılarda Bölme | 7. Sınıf Tam Sayılarda Bölme Testleri Çöz | Teste Başla |
| 19. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Çözümlü Sorular | Teste Başla |
| 20. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Testleri | Teste Başla |
| 21. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Test | Teste Başla |
| 22. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Testi | Teste Başla |
| 23. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Online Test | Teste Başla |
| 24. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Testleri | Teste Başla |
| 25. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Test | Teste Başla |
| 26. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Testi | Teste Başla |
| 27. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Online Test | Teste Başla |
| 28. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Test Çöz | Teste Başla |
7.Sınıf Matematik Tablo ve Grafikler Testleri 5
7.Sınıf Matematik Tablo ve Grafikler Testi
6. Sınıf Matematik Tablo ve Grafikler
# 6. Sınıf Matematik Tablo ve Grafikler Konu Anlatımı
# 6. Sınıf Matematik Tablo ve Grafikler 2
# 6. Sınıf Matematik Tablo ve Grafikler 3
# 6. Sınıf Matematik Tablo ve Grafikler 4
# 6. Sınıf Matematik Tablo ve Grafikler 5
# 6. Sınıf Matematik Tablo ve Grafikler 6
# 6. Sınıf Matematik Tablo ve Grafikler 7
# 6. Sınıf Matematik Tablo ve Grafikler 8
# 6. Sınıf Matematik Tablo ve Grafikler 9
# 6. Sınıf Matematik Tablo ve Grafikler 10
# 6. Sınıf Matematik Tablo ve Grafikler 11
# 6. Sınıf Matematik Tablo ve Grafikler 12
# 6. Sınıf Matematik Tablo ve Grafikler 13
# 6. Sınıf Matematik Tablo ve Grafikler 14
# 6. Sınıf Matematik Tablo ve Grafikler 15
# 6. Sınıf Matematik Tablo ve Grafikler 16
# 6. Sınıf Matematik Tablo ve Grafikler 17
# 6. Sınıf Matematik Tablo ve Grafikler 18
# 6. Sınıf Matematik Tablo ve Grafikler 19
Kategoriler: Matematik Etiketler: 7. sınıf matematik tablo ve grafikler testini çöz, 7. sınıf matematik tablo ve grafikler testleri
7.Sınıf Matematik Tablo ve Grafikler Deneme Sınavı 2
7.Sınıf Matematik Tablo ve Grafikler Testi
6. Sınıf Matematik Tablo ve Grafikler
# 6. Sınıf Matematik Tablo ve Grafikler Konu Anlatımı
# 6. Sınıf Matematik Tablo ve Grafikler 1
# 6. Sınıf Matematik Tablo ve Grafikler 2
# 6. Sınıf Matematik Tablo ve Grafikler 3
# 6. Sınıf Matematik Tablo ve Grafikler 4
# 6. Sınıf Matematik Tablo ve Grafikler 5
# 6. Sınıf Matematik Tablo ve Grafikler 6
# 6. Sınıf Matematik Tablo ve Grafikler 7
# 6. Sınıf Matematik Tablo ve Grafikler 8
# 6. Sınıf Matematik Tablo ve Grafikler 9
# 6. Sınıf Matematik Tablo ve Grafikler 10
# 6. Sınıf Matematik Tablo ve Grafikler 11
# 6. Sınıf Matematik Tablo ve Grafikler 12
# 6. Sınıf Matematik Tablo ve Grafikler 13
# 6. Sınıf Matematik Tablo ve Grafikler 14
# 6. Sınıf Matematik Tablo ve Grafikler 16
# 6. Sınıf Matematik Tablo ve Grafikler 17
# 6. Sınıf Matematik Tablo ve Grafikler 18
# 6. Sınıf Matematik Tablo ve Grafikler 19
Kategoriler: Matematik Etiketler:
7.Sınıf Matematik Tablo ve Grafikler Deneme Sınavı
7.Sınıf Matematik Tablo ve Grafikler Testi
6. Sınıf Matematik Tablo ve Grafikler
# 6. Sınıf Matematik Tablo ve Grafikler Konu Anlatımı
# 6. Sınıf Matematik Tablo ve Grafikler 1
# 6. Sınıf Matematik Tablo ve Grafikler 2
# 6. Sınıf Matematik Tablo ve Grafikler 3
# 6. Sınıf Matematik Tablo ve Grafikler 4
# 6. Sınıf Matematik Tablo ve Grafikler 5
# 6. Sınıf Matematik Tablo ve Grafikler 6
# 6. Sınıf Matematik Tablo ve Grafikler 7
# 6. Sınıf Matematik Tablo ve Grafikler 8
# 6. Sınıf Matematik Tablo ve Grafikler 9
# 6. Sınıf Matematik Tablo ve Grafikler 10
# 6. Sınıf Matematik Tablo ve Grafikler 11
# 6. Sınıf Matematik Tablo ve Grafikler 12
# 6. Sınıf Matematik Tablo ve Grafikler 13
# 6. Sınıf Matematik Tablo ve Grafikler 15
# 6. Sınıf Matematik Tablo ve Grafikler 16
# 6. Sınıf Matematik Tablo ve Grafikler 17
# 6. Sınıf Matematik Tablo ve Grafikler 18
# 6. Sınıf Matematik Tablo ve Grafikler 19
7.Sınıf Matematik Tablo ve Grafikler Konu Tarama
7.Sınıf Matematik Tablo ve Grafikler Testi
6. Sınıf Matematik Tablo ve Grafikler
# 6. Sınıf Matematik Tablo ve Grafikler Konu Anlatımı
# 6. Sınıf Matematik Tablo ve Grafikler 1
# 6. Sınıf Matematik Tablo ve Grafikler 2
# 6. Sınıf Matematik Tablo ve Grafikler 3
# 6. Sınıf Matematik Tablo ve Grafikler 4
# 6. Sınıf Matematik Tablo ve Grafikler 5
# 6. Sınıf Matematik Tablo ve Grafikler 6
# 6. Sınıf Matematik Tablo ve Grafikler 7
# 6. Sınıf Matematik Tablo ve Grafikler 8
# 6. Sınıf Matematik Tablo ve Grafikler 9
# 6. Sınıf Matematik Tablo ve Grafikler 10
# 6. Sınıf Matematik Tablo ve Grafikler 11
# 6. Sınıf Matematik Tablo ve Grafikler 12
# 6. Sınıf Matematik Tablo ve Grafikler 14
# 6. Sınıf Matematik Tablo ve Grafikler 15
# 6. Sınıf Matematik Tablo ve Grafikler 16
# 6. Sınıf Matematik Tablo ve Grafikler 17
# 6. Sınıf Matematik Tablo ve Grafikler 18
# 6. Sınıf Matematik Tablo ve Grafikler 19