8. Sınıf Matematik Çok Küplü Yapılar, Çok Yüzlüler ve Simetri Konu Anlatımı
Çok Küplü Yapılar, Çok Yüzlüler ve Simetri
Çok Küplüler
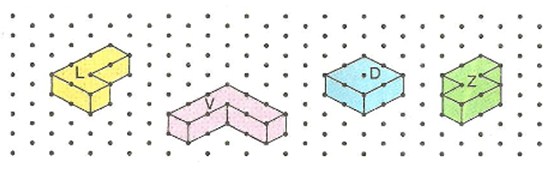
İzometrik kağıt, çok küplü modelleri kullanılarak geometrik yapıların çizilebildiği bir geometri materyaldir.
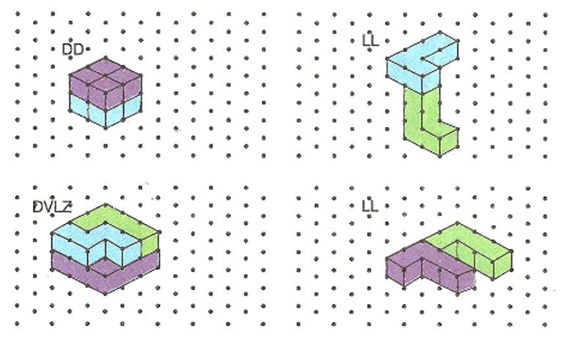
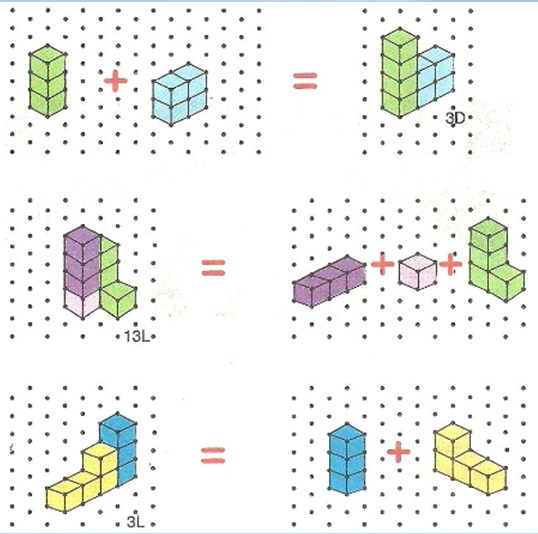
Yukarıda L, D, V ve Z çok küplü modelleri vardır. Bu modellerle farklı geometrik yapılar oluşturulabilir :
L, D, V ve Z çok küplü modellerinin yanında 1, 2, 3 modelleri de vardır.
Çok Yüzlüler
Geometrik cisimlerde de platoniklik olur mu? Demeyin:
“Platonik Cisimler” olarak bilinen düzgün çok yüzlüler adını ünlü filozof matematikçi Platon’dan almıştır.
Eflatun’un öğrencisi olan Platon, matematiğin gelişmesinde rehberlik etmiş, dönemindeki matematiksel çalışmaların çoğunun merkezinde yer almıştır. Ayrıca Platon’un eğitim verdiği okulun kapısına “Geometri bilmeyen giremez.” Yazdırması geometriye ne kadar önem verdiğinin ispatıdır.
Platon “Timaeus” adlı eserinde düzgün katı cisimlerle ilgili düşüncesini açıklamıştır. Platon’a göre 5 geometrik cisim şunlardır :
1. Düzgün dört yüzlü
2. Düzgün altı yüzlü
3. Düzgün sekiz yüzlü
4. Düzgün on iki yüzlü
5. Düzgün yirmi yüzlü
Platonik cisimlerden düzgün dört yüzlü olarak bilinen katı cisim piramit, düzgün altı yüzlü olarak bilinen katı cisim ise küptür.
Platonik cisimlerin özelliklerini öğrenmek için aşağıdaki tablolardan yararlanılabilir.
Platonik Cisimlerin Yüzeyleri : Düzgün dört yüzlü, 4 eşkenar üçgenden, düzgün sekiz yüzlü, 8 eşkenar üçgenden; küp, 6 eş kareden; düzgün on iki yüzlü, 12 beşgenden; düzgün yirmi yüzlü, 20 eşkenar üçgenden oluşur.
Şekildeki düzgün sekiz yüzlünün yüksekliği, bir düzgün dört yüzlünün bir kenar uzunluğuna eşittir. |AB| = 12 cm olduğuna göre düzgün dört yüzlünün yüksekliği kaç santimetredir?
Düzgün sekiz yüzlünün yüksekliği
Dört yüzlünün bir kenar uzunluğudur. Düzgün dört yüzlünün yüksekliği,
Simetri
Çevremizdeki nesnelerin her biri simetrik midir? Simetri bütün geometrik şekiller için geçerli midir? Uzayda simetriden söz edilebilir mi?
Geometrik cisimler için simetri, belli bir eksen etrafındaki dönme hareketidir.
• Küp, kendi ekseni etrafında 90° lik dönmelerinde konum değiştirmez.
• Küp ve dikdörtgenler prizması karşılıklı yüzlerin paralel olan kenarının orta dikmelerinden ve paralel olan yüzey köşegenlerinden geçen düzlemlere göre simetriktir.
• Eşkenar üçgen prizma, taban merkezinden geçen eksen etrafında 120° lik dönmelerinde değişmez.
• Küre, çaplarından her biri etrafındaki dönmelerinde sabit kalır. Çaplarından geçen her düzleme göre simetriktir.
| 8. Sınıf Çok Küplü Yapılar Çok Yüzlüler ve Simetri | Açıklama | Test Linki |
| 1. Çok Küplü Yapılar Çok Yüzlüler ve Simetri | 8. Sınıf Matematik Çok Küplü Yapılar Çok Yüzlüler ve Simetri Testleri | Teste Başla |
| 2. Çok Küplü Yapılar Çok Yüzlüler ve Simetri | 8. Sınıf Matematik Çok Küplü Yapılar Çok Yüzlüler ve Simetri Test | Teste Başla |
| 3. Çok Küplü Yapılar Çok Yüzlüler ve Simetri | 8. Sınıf Matematik Çok Küplü Yapılar Çok Yüzlüler ve Simetri Testi | Teste Başla |
| 4. Çok Küplü Yapılar Çok Yüzlüler ve Simetri | 8. Sınıf Matematik Çok Küplü Yapılar Çok Yüzlüler ve Simetri Online Test | Teste Başla |
| 5. Çok Küplü Yapılar Çok Yüzlüler ve Simetri | 8. Sınıf Matematik Çok Küplü Yapılar Çok Yüzlüler ve Simetri Genel Değerlendirme | Teste Başla |
| 6. Çok Küplü Yapılar Çok Yüzlüler ve Simetri | 8. Sınıf Matematik Çok Küplü Yapılar Çok Yüzlüler ve Simetri Konu Tarama | Teste Başla |
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Perspektif Çizimi ve Ara Kesitler Konu Anlatımı
Perspektif Çizimi
Perspektifte, cisimler bizden uzaklaştıkça küçülmüş ve solmuş gibi görünür.
Zeminin bittiği yerde, gökyüzüyle birleşen çizgiye “ufuk çizgisi” denir.
Gözümüzden uzaklaştıkça birleşiyormuş gibi görünen çizgilere “kaybolunan doğrular”, kaybolunan doğruların birleşiyormuş gibi göründüğü noktaya da “kaybolunan nokta” denir. Gökyüzüyle birleşen çizgiye “ufuk çizgisi” denir.
Bir Nokta Perspektifi
Ön yüzü ve üst yüzü görünen cisimlerin perspektifini çizme
Perspektif çizimi yapılacak cismi ön yüzü ile üst tabanı görünecek şekilde yerleştirelim.
Kutunun ön yüzü için kağıt düzlemine bir dikdörtgen çizelim.
Dikdörtgenin üst tarafına dikdörtgene paralel olacak şekilde bir doğru çizelim.
Dikdörtgenin tabanının orta noktası hizasında olacak şekilde, doğru üzerinde bir nokta belirleyelim.
Belirlediğimiz noktaya dikdörtgenin dört köşesinden noktalı doğru parçaları çizelim.
Noktalı doğru parçaları arasında kalacak ve yatay doğruya paralel olacak şekilde doğru parçası çizip kutunun üst ayrıtlarını oluşturalım.
Arkada saklı duran diğer dikey ve yatay doğru parçalarını noktalı olarak çizelim.
Ön Yüzü, Alt Yüzü ve Sol Yüzü Görünen Cisimlerin Perspektifini Çizme
Perspektif çizimi yapılacak cismi ön yüzü, alt tabanı ve sol yüzü görünecek şekilde yerleştirelim.
Kutunun ön yüzü için kağıt düzlemine bir dikdörtgen çizelim.
Dikdörtgenin alt tarafına dikdörtgene paralel olacak şekilde bir doğru çizelim.
Dikdörtgenin sol tarafından olacak şekilde, doğru üzerinde bir nokta belirleyelim.
Belirlediğimiz noktaya dikdörtgenin dört köşesinden noktalı doğru parçaları çizelim.
Noktalı doğru parçaları arasında kalacak ve yatay doğruya paralel olacak şekilde doğru parçası çizip kutunun alt ayrıtlarını oluşturalım.
Arkada saklı duran diğer dikey ve yatay doğru parçalarını noktalı olarak çizelim.
Fazlalıkları silerek çizimi tamamlayalım.
Ön Yüzü, Üst Yüzü ve Sağ Yüzü Görünen Cisimlerin Perspektifini Çizme
Perspektif çizimi yapılacak cismi ön yüzü, üst tabanı ve sağ yüzü görünecek şekilde yerleştirelim.
Perspektif çizimi yapılacak cismi ön yüzü, üst tabanı ve sağ yüzü görünecek şekilde yerleştirelim.
Dikdörtgenin üst tarafına dikdörtgene paralel olacak şekilde bir doğru çizelim.
Dikdörtgenin sağ tarafında olacak şekilde, doğru üzerinde bir nokta belirleyelim.
Belirlediğimiz noktaya dikdörtgenin dört köşesinden noktalı doğru parçaları çizelim.
Noktalı doğru parçaları arasında kalacak ve yatay doğruya paralel olacak şekilde doğru parçası çizip kutunun üst ayrıtlarını oluşturalım.
Arkada saklı duran diğer dikey ve yatay doğru parçalarını noktalı olarak çizelim.
Fazlalıkları silerek çizimi tamamlayalım.
Not : Prizma modelinin ön yüzü, resmin (çizimin) düzlemine paralel olarak yapılıyorsa bu perspektif çizim tipine “bir nokta perspektifi” denir.
Kaybolunan nokta, prizmaya sağdan bakıldığında ufuk çizgisi üzerinde ve prizmanın sağında; soldan bakıldığında ise solundadır. Bu durum prizmaya alttan ve üstten bakıldığında değişmez.
İki Nokta Perpektifi
Üst Yüzü ve Yan Yüzleri Görünen Cisimlerin Perspektifini Çizme
Perspektif çizimi yapılacak cismi aynı köşeden kesişen üç yüzünden üst yüzü ile sağ ve sol yanı görünecek şekilde yerleştirelim.
Kutunun kağıt düzlemine paralel olmayan ön yüzündeki ayrıt için dikey bir doğru parçası çizelim.
Dikey doğru parçasının üst tarafına yatay bir doğru çizelim.
Doğrunun sağ ve sol tarafında birer nokta belirleyelim.
Dikey doğru parçasının uçlarını noktalı doğrularla doğru üzerindeki noktalarla birleştirelim.
Cismin uzunluğu ve genişliği için noktalı doğrular arasına dikey doğrular çizelim.
Cismin arkasında kalan görünmeyen ayrıtlarını çizeceğimiz doğruları çizelim.
Üst tabanı ve görünmeyen yüzleri oluşturalım.
Fazlalıkları silerek çizimi tamamlayalım.
Alt Yüzü ve Yan Yüzleri Görünen Cisimlerin Perspektifini Çizme
Perspektif çizimi yapılacak cismi aynı köşeden kesişen üç yüzünden alt yüzü ile sağ ve sol yanı görünecek şekilde yerleştirelim.
Kutunun kağıt düzlemine paralel olmayan ön yüzündeki ayrıt için dikey bir doğru parçası çizelim.
Dikey doğru parçasının alt tarafına yatay bir doğru çizelim.
Doğrunun sağ ve sol tarafında birer nokta belirleyelim.
Dikey doğru parçasının uçlarını noktalı doğrularla doğru üzerindeki noktalarla birleştirelim.
Çok Yüzlüler ve Ara Kesitler
Aşağıdaki şekillerde değişik çok yüzlüler görülmektedir.
Elmas ve pırlantalarda çok yüzlülere örnek olarak verilebilir. Elmas ve pırlanta aynı taşın farklı kesim şekilleridir. Elmasın alt kısmı düz, yüz sayısı ise 12 ile 37 arasında değişmektedir. Daha ince işçiliğe sahip pırlantanın alt kısmı kubbe gibi, yüz sayısı ise genellikle 57’dir.
Kesik Cisimler
Küpün Bir Düzlemle Kesişim
Şekildeki küp tabanına dik bir düzlemle kesilirse oluşan kesit alanı bir karedir.
Şekildeki küp A, B, C noktalarından geçen bir düzlemle kesilirse oluşan kesit alanı bir eşkenar üçgendir.
Şekildeki küp A, B, C, D, E noktalarından geçen bir düzlemle kesilirse oluşan kesit alanı bir beşgendir.
|AD| = |DC| = |DB| olduğunda şekildeki küp A, B, C noktalarından geçen bir düzlemle kesilirse oluşan kesit alanı bir eşkenar üçgendir.
Şekildeki küp A, B, C, D, E, F noktalarından geçen bir düzlemle kesilirse oluşan kesit alanı bir altıgendir.
Şekildeki küp A, B, C noktalarından geçen bir düzlemle kesilirse oluşan kesit alanı bir çeşitkenar üçgendir.
| 8. Sınıf Perspektif Çizimi ve Ara Kesitler | Açıklama | Test Linki |
| 1. Perspektif Çizimi ve Ara Kesitler | 8. Sınıf Matematik Perspektif Çizimi ve Ara Kesitler Testleri | Teste Başla |
| 2. Perspektif Çizimi ve Ara Kesitler | 8. Sınıf Matematik Perspektif Çizimi ve Ara Kesitler Test | Teste Başla |
| 3. Perspektif Çizimi ve Ara Kesitler | 8. Sınıf Matematik Perspektif Çizimi ve Ara Kesitler Testi | Teste Başla |
| 4. Perspektif Çizimi ve Ara Kesitler | 8. Sınıf Matematik Perspektif Çizimi ve Ara Kesitler Online Test | Teste Başla |
| 5. Perspektif Çizimi ve Ara Kesitler | 8. Sınıf Matematik Perspektif Çizimi ve Ara Kesitler Genel Değerlendirme | Teste Başla |
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Prizma, Piramit, Koni ve Kürenin Hacmi Konu Anlatımı
Prizma, Piramit, Koni ve Kürenin Hacmi
Geometrik Cisimlerin Hacimleri
Evrendeki tüm nesneler bir yer kaplar mı? Dünya’nın hacmi var mıdır, hiç düşündünüz mü? Dünya’nın hacmi yaklaşık olarak 1.803.207,000 km3 tür.
Peki sıvıların hacmi var mıdır? Sıvıların hacmi, içindeki bulunduğu bölgenin hacmidir.
Bir havuzun alabileceği suyun hacminin hesaplanabilmesi için en, boy ve derinlik uzunluklarının bilinmesi gereklidir.
Ancak havuz gibi 3 boyutlu cisimlerin hacmi hesaplanabilir. Kare prizma, silindir gibi geometrik cisimlerin hacimleri boyutları kullanılarak hesaplanır.
Dik Prizmaların Hacimleri
Yukarıdaki dikdörtgenler prizması eş birim küplerden oluşmuştur. Bu prizmanın hacmini bulmak için birim küpler sayılır. Sayma sonucunda dikdörtgenler prizmasının hacmi 60 br3 olarak bulunur. Verilen prizmanın hacmini bulmak için birim küpleri saymak yerine kısa bir yol var mıdır?
Prizmanın taban alanını bulup yükseklikle çarparsanız yine aynı sonucu elde edersiniz.
Taban ayrıtları 5 br, 3 br ve yüksekliği 4 br olan dikdörtgenler prizmasının taban alanı
Ta = 3 br . 5 br = 15 br2 dir.
Dikdörtgenler prizmasının hacmi ise,
V = 15 br2 . 4 br = 60 br3 bulunur.
Dik prizmaların hacimlerinin hesaplanmasında dikdörtgenler prizmasının hacminden yararlanılır.
Genel olarak dik prizmaların hacmi V = Ta . h bağıntısı ile bulunur.
Örnek : Taban alanı 48 cm2 ve yüksekliği 12 cm olan dik prizmanın hacmi kaç santimetre küptür?
V = Ta . h
V = 48 . 12
V = 576 cm2
Örnek : Hacmi 144 m3 olan dik prizma şeklindeki havuzun yüksekliği 3 m dir. Bu havuzun taban alanı kaç metre karedir?
V = Ta . h
144 = Ta . 3
Ta = 48 m2
Dikdörtgenler Prizmasının Hacmi
Yukarıdaki havuz dikdörtgenler prizması şeklindedir. Bu havuzun hacminin bulunması için hangi uzunluklarının bilinmesi gereklidir?
Dik prizmaların hacmi Ta. h olduğundan havuzun en, boy ve derinlik uzunluklarının bilinmesi gereklidir.
Ayrıt uzunlukları a, b ve ce olan dikdörtgenler prizmasının hacmi :
V = Ta. c’dir
V = a.b.c
Kare Dik Prizmanın Hacmi
Yukarıdaki bidon kare dik prizma şeklindedir. Bu bidonun hacminin bulunması için tabanındaki karesel bölgenin alanına ve yüksekliğine ihtiyaç vardır.

Taban ayrıt uzunluğu a ve yüksekliği h olan kare dik prizmanın hacmi : V = Ta . h ‘dir.
V = a2 . h
Örnek : Taban ayrıt uzunluğu 15 cm, yüksekliği 25 cm olan kare dik prizma şeklindeki abajurun hacmi kaç santimetre küptür?
T a = a2
T a = 152
T a = 225 cm2
V = T a . h
V = 225 . 25
V = 5625 cm2
Üçgen Dik Prizmanın Hacmi
Üçgen dik prizmanın hacminin bulunması için tabanındaki üçgensel bölgenin alanına ve prizmanın yüksekliğine ihtiyaç vardır.
Tabanındaki üçgensel bölgenin bir kenar uzunluğu a ve bu kenara ait yüksekliği h a prizma yüksekliği h olan üçgen dik prizmanın hacmi
V = T a . h’dir.
Dik Silindirin Hacmi
Bir prizmanın tabanındaki düzgün çokgenin kenar sayısı çok artırıldığında tabanı daireye yaklaşır.
Dik silindir, tabanı daire olan dik prizma olduğundan hacmi V = T a. H bağıntısı ile bulunur.
Taban yarıçapı r ve yüksekliği h olan dik silindirin hacmi :
V = π .r2 . h
Dik Piramitlerin Hacmi
Aynı taban ve yükseklikte dik prizma şeklinde kap ile dik piramit şeklinde kap düşünün. Prizma şeklindeki kabın hacmi piramit şeklindeki kabın hacminin kaç katıdır.
Piramit modelini su ile doldurup prizma modeline boşaltın. Prizma modeli doluncaya kadar bu işlemi tekrarlayın. Sonra aynı işlemi tersten yapın. Prizma modelindeki suyu piramit modeline boşaltın. Prizma modelindeki su bitene kadar bu işlemi tekrarlayın.
Yaptığınız işlemler sonrasında eş taban ve eş yüksekliğe sahip prizmanın hacminin, piramidin hacminin 3 katı olduğunu bulursunuz.
Dik prizmaların hacmi
V = T a . h olduğundan dik piramitlerin hacmi :
Dik Dairesel Koninin Hacmi
Aynı taban ve yükseklikte dik dairesel koni şeklinde vazo ile dik silindir şeklinde vazo düşünün. Dik silindir şeklindeki vazonun hacmi dik dairesel koni şeklindeki vazonun hacminin kaç katıdır?
Dik dairesel koni modelini su ile doldurup dik silindir modeline boşaltın. Dik silindir modeli doluncaya kadar bu işlemi tekrarlayın.
Sonra aynı işlemi tersten yapın. Dik silindir modelindeki suyu dik dairesel koni modeline boşaltın. Dik silindir modelindeki su bitene kadar bu işlemi tekrarlayın.
Yaptığınız işlemler sonrasında eş taban ve eş yüksekliğe sahip dik silindirin hacminin, dik dairesel koninin hacminin 3 katı olduğunu bulursunuz.
R yarıçaplı ve yüksekliği h olan dik silindirin hacmi :
V = T a . h = π . r2 . h olduğundan r yarıçaplı ve yüksekliği h olan dik dairesel koninin hacmi :
Kürenin Hacmi
Taban yarıçapı r, yüksekliği 2r olan dik silindir şeklindeki kabı tamamen su ile doldurun. Bu kabın içine r yarıçaplı küre şeklinde bilyeyi tam batıncaya kadar bastırın. Taşan suyu başka bir kaba alın.
Bilyeyi serbest bırakın ve dik silindir şeklindeki kapta kalan su seviyesini işaretleyin. Taşan suyun hacmi bilyenin hacmine eşittir.
Elde edilen sonuçlar sonrasında kürenin hacminin, dik silindirin hacminin 2/3’üne eşit olduğunu bulursunuz.
r yarıçaplı ve yüksekliği 2r olan dik silindirin hacmi :
V = π . r2 . 2r
r yarıçaplı kürenin hacmi :
Koninin hacminin 3 katı olduğunu bulursunuz.
r yarıçapı ve yüksekliği h olan dik silindirin hacmi :
V = T a . h = π . r2 . h olduğundan r yarıçaplı ve yüksekliği h olan dik dairesel koninin hacmi :
| 8. Sınıf Prizma Piramit Koni ve Kürenin Hacmi | Açıklama | Test Linki |
| 1. Prizma Piramit Koni ve Kürenin Hacmi | 8. Sınıf Matematik Prizma Piramit Koni ve Kürenin Hacmi Testleri | Teste Başla |
| 2. Prizma Piramit Koni ve Kürenin Hacmi | 8. Sınıf Matematik Prizma Piramit Koni ve Kürenin Hacmi Test | Teste Başla |
| 3. Prizma Piramit Koni ve Kürenin Hacmi | 8. Sınıf Matematik Prizma Piramit Koni ve Kürenin Hacmi Testi | Teste Başla |
| 4. Prizma Piramit Koni ve Kürenin Hacmi | 8. Sınıf Matematik Prizma Piramit Koni ve Kürenin Hacmi Online Test | Teste Başla |
| 5. Prizma Piramit Koni ve Kürenin Hacmi | 8. Sınıf Matematik Prizma Piramit Koni ve Kürenin Hacmi Test Çöz | Teste Başla |
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Küreyi Tanıyalım Konu Anlatımı
Küreyi Tanıyalım
Futbol topu, yer küre, bilyeler … küre biçimindeki nesnelerdir.
Kürenin yüzeyindeki iki noktayı birleştiren doğru parçası kürenin kirişleri, merkezden geçen kiriş kürenin çapıdır. Kürenin merkezinden geçen bir düzlemde kürenin ara kesitinden oluşan çember kürenin büyük çemberidir.
Kürenin büyük çemberinin yarıçapı, kürenin yarıçapına eşittir.
[KM] : kiriş
[AB] : çap
[OB] : büyük çemberin yarıçapı
Küre ile Düzlemin Ara Kesiti :
Küre yüzeyi ile bir düzlemin ara kesiti bir çemberdir.
Küre ile bir düzlemin ara kesiti bir dairedir.
Bir küre bir düzlemde kesildiğinde kesit dairenin yarıçapı r, kesit dairenin merkezden uzaklığı d, kürenin yarıçapı R olmak üzere
r2 + d2 = R2 bağıntısı geçerlidir.
Örnek :
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Koniyi Tanıyalım Konu Anlatımı
Koniyi Tanıyalım
Dik Koni :
Partilerde, kutlamalarda kullandığınız ilginç şapkalar, yağ hunileri, kurşun kaleminizin sivriltilmiş ucu, dondurmanızın külahı hangi geometrik cisime benzer?
Koninin tepe noktasından taban düzlemine inilen dikme cisim yüksekliği, tepe noktasını taban çevresi üzerindeki bir noktaya birleştiren doğru parçası ana doğrusudur.
h : [OT] : cisim yüksekliği
a : [TC] : ana doğru
r : [OC] : yarıçap
Örnek : Yarıçapı 10 cm olan bir dik koninin merkez açısının ölçüsü 72° dir. Koninin ana doğrusu ve yüksekliği kaç santimetredir?
Dik Koni ve Kesik Koni Oluşturma
1. Bir dik üçgenin dik kenarlarından biri etrafında 360° döndürülmesiyle bir dik koni oluşur.
2. Bir dik yamuğun yüksekliği etrafında 360° döndürülmesiyle bir kesik koni oluşur.
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Piramitleri Tanıyalım Konu Anlatımı
Piramitleri Tanıyalım
Piramitler ve Özellikleri
Piramitler ile prizmalar arasındaki benzerlik ve farklılıklar nelerdir?
Piramitler de prizmalar gibi tabanlarındaki çokgene göre adlandırılırlar: üçgen piramit, kare piramit …
Piramidin tabanındaki çokgenin köşelerinin birleştirildiği T noktası piramidin tepe noktası ya da tepesi, tepe noktasından taban düzlemine inilen dikme piramidin cisim yüksekliği, yanal yüzeyini oluşturan üçgenlerin yükseklikleri piramidin yanal yüzey yükseklikleridir.
Taban yüzey : ABCD
Yanal yüzeyleri : TBC, TAB, TDC, TAD
Yanal ayrıtları : [TB], [TD], [TA], [TC]
Taban ayrıtları : [AD], [DC], [AB], [BC]
Köşeleri : A, B, C, D
Yanal yüzey yüksekliği : [TF]
Bir piramitteki yanal yüzey sayısı, taban ayrıtı sayısına eşittir. Üçgen piramidin 3 taban ayrıtı, 3 yanal yüzeyi vardır.
Düzgün altıgen piramidin 6 taban ayrıtı, 6 yanal yüzeyi vardır.
Piramit :
Bir çokgensel bölgenin köşelerinin bir tepe noktasında birleştirilmesiyle oluşan kapalı geometrik cisimlerdir.
Düzgün Piramit :
Tabanı düzgün çokgen, yanal yüzeyleri eş ikizkenar üçgenler olan piramitlerdir.
Kesik Piramit :
Bir piramit tabanına paralel bir düzlemle kesildiğinde taban ile düzlem arasında kalan kısımdır.
Örnek : Taban çevresi 64 cm olan şekildeki kare piramidin yanal yüzey yüksekliği 10 cm’dir.
Buna göre piramidin cisim yüksekliği kaç santimetredir?
KLMN karesinin çevresi 64 cm olduğuna göre taban ayrıtı,
64 : 4 = 16 cm’dir.
|HR| = |KL| : 2 = 8 cm, yanal yüzey yüksekliği |TR| = 10 cm olduğuna göre THR dik üçgeninde Pisagor bağıntısı kullanılır. Buna göre piramidin cisim yüksekliği
|TH|2 + |HR|2 = |TR|2 eşitliğinde
|TH|2 = 102 – 82
= 100 – 64 = 36
|TH| = 6 cm bulunur.
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Prizmaları Tanıyalım Konu Anlatımı
Prizmaları Tanıyalım
Prizmalar ve Özellikleri
İçinde yaşadığımız binalar, evlerimizin odaları, sınıfımız, defterimiz, kullandığımız birçok eşya modeli farklı biçimlerdeki prizmalara örnek oluşturur.
Prizmalar dik veya eğik oluşlarının dışında tabanlarındaki çokgene göre adlandırılırlar : üçgen prizma, kare prizma …
Bir prizmanın taban düzlemi dışındaki yüzeyleri yanal yüzeyleri, yanal yüzeylerinin ara kesiti olan doğru parçaları yanal ayrıtları, prizmanın tabanlarını oluşturan doğru parçaları taban ayrıtların kesiştiği noktalar prizmanın köşeleri, taban düzlemleri arasındaki uzaklık yükseklikleridir.
Taban yüzeyler : ABC, DEF
Yanal yüzeyleri : DECA, FECB, ABFD
Yanal ayrıtları : [AD], [BF], [CE]
Taban ayrıtları : [AC], [AB], [BC]
Köşeleri : A, B, C, D, E, F
Dik Prizmalarda
• Yan yüzler dikdörtgendir.
• Alt ve üst tabanlar birbirine eştir.
• Prizmanın tabanlarından biri enine kesittir.
• Prizmalarda enine kesitler birbirine ve tabanlara eştir.
• Yanal ayrıtları, tabanlara diktir.
Eğik Prizmalarda
• Yan yüzler paralelkenardır.
• Bir eğik prizma yanal ayrıtlarına dik bir düzlemle kesilirse dik kesiti elde edilir.
• Dik kesit, yanal yüzeylerin yüksekliğidir.
• Eğik prizmada dik kesit tabanlara eş değildir.
Prizma : Paralel iki düzlemde birbirine eş iki çokgensel bölgenin eş kenarlarının karşılıklı doğru parçasıyla birleştirilmesiyle oluşan kapalı geometrik cisimlerdir.
Dik Prizma : Yan yüzleri tabanlara dik olan prizmalardır.
Eğik Prizma : Yan yüzleri tabanlara dik olmayan prizmalardır.
Eğik Prizmalarda Açı : bir eğik prizmada yanal ayrıt ile taban düzlemi arasında belirli bir açı vardır. Bu açı a ile gösterilirse,
Sina = yükseklik / yanal ayrıt oranı ile hesaplanır.
Dikdörtgenler Prizması
Dikdörtgenler prizmasının
• 6 yüzeyi vardır. Karşılıklı yüzeyleri birbirine eş dikdörtgendir.
• 12 ayrıtı vardır. Karşılıklı ayrıtları paraleldir ve uzunlukları eşittir.
• 8 köşesi vardır. Bir köşesinde birleşen ayrıtları; uzunluk, genişlik ve yüksekliktir.
Dikdörtgenler prizmasının bir köşesinde birleşen ayrıtlar a, b ve c olsun.
Dikdörtgenler prizmasının yüzey köşegenlerinden biri [DB], cisim köşegenlerinden biri [BD]’dır.
BDC üçgeninde Pisagor bağıntısı kullanılırsa ![]()
Örnek :
Şekildeki dikdörtgenler prizmasında boyalı bölgenin alanı 150 cm2 ‘dir. |AB| = 24 cm olduğuna göre prizmanın ayrıt uzunlukları toplamı kaç santimetredir?
Çözüm : Boyalı bölge dikdörtgen olduğundan |AB’| = 150 : 6 = 25 cm’dir.
ABB’ üçgeninde Pisagor bağıntısı kullanılarak
|AB’| = |AB| + |BB| eşitliğinden |BB| = 7 cm bulunur.
Prizmanın ayrıtları a = 24 cm, b = 6 cm ve c = 7 cm’dir.
Ayrıt uzunlukları toplamı
4 . (a + b + c) = 4 . (24 + 6 + 7)
= 148 cm’dir.
Yüzey ve Cisim Köşegeni : Bir prizmanın yüzey köşegeni e, cisim köşegeni f veya k harfiyle gösterilir.
Bir prizmada yüzey köşegeni, cisim köşegeninden daha kısadır.
Bir dikdörtgenler prizmasının 12 yüzey köşegeni, 4 cisim köşegeni vardır.
Kare Prizma :
Kare prizmanın
• 6 yüzeyi vardır. Alt ve üst tabanları birbirine eş kare, yan yüzeyleri ise birbirine eş dikdörtgenlerdir.
• 12 ayrıtı, 8 köşesi vardır. Bir köşede birleşen üç ayrıt birbirine diktir.
Kare prizmanın bir köşesinde birleşen ayrıtlar a ve b olsun. Taban ayrıtının uzunluğu a olan kare prizmada yüzey köşegeni.
Üçgen Prizma
Üçgen prizmanın
5 yüzeyi vardır. Alt ve üst tabanları birbirine eş üçgen, yan yüzeyleri ise dikdörtgenlerdir.
9 ayrıtı, 6 köşesi vardır. Karşılıklı ayrıtları birbirine paralel ve uzunlukları eşittir. Yanal ayrıtları aynı zamanda üçgen prizmanın yüksekliğidir.
Üçgen prizmanın alt ve üst tabanlarındaki üçgenlerin köşegeni olmadığından bu yüzeylerde yüzey köşegeninden bahsedilemez.
Yanal yüzeylerdeki dikdörtgenlerde yüzey köşegeni hesabı yapılabilir.
Örnek :
Şekildeki üçgen prizmada |AC| = 3 cm olduğuna göre prizmanın ayrıt uzunlukları toplamı kaç santimetredir?
ACB dik üçgeninde |AC| = 3 cm, |CB| = 4 cm olduğundan Pisagor bağıntısı kullanılarak
|AB|2 = |AC|2 + |CB|2
|AB|2 = 9 + 16 = 25
|AB| = 5 cm bulunur.
Prizmanın ayrıt uzunlukları toplamı :
2 . (|AB| + |AB| + |BC|) + 4.|BE|
2.(3+4+5)+4.10=64 cm’dir.
Üçgen Prizma Çeşitleri :
Bir üçgen prizmanın taban ayrıtları a, b ve c; yüksekliği h olmak üzere ayrıt uzunlukları toplamı 2(a+b+c)+4h ile hesaplanır.
Düzgün Altıgen Prizma : Düzgün altıgen prizmanın,
8 yüzeyi vardır. Alt ve üst tabanları birbirine eş altıgen, yan yüzeyleri ise birbirine eş dikdörtgenlerdir.
18 ayrıtı 12 köşesi vardır. Yanal ayrıtlar prizmanın yükseklikleridir. Taban ayrıtlarının uzunlukları birbirine yanal ayrıtlarının uzunlukları birbirine eşittir.
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Standart Sapma Konu Anlatımı
Standart Sapma
Ahmet Bey’e babasından 10 bin TL miras kalmıştır. Ahmet Bey, bu parayı bono ya da altın alarak değerlendirmek istiyor.
Aşağıdaki grafikler altın ve bononun şubat ayının 2. Haftasındaki seyrini göstermektedir.
Bu grafiklere göre, sizce Ahmet Bey altına mı, Ulusal Endeske mi yatırım yapmalıdır?
Etkinlik
Hangi Bahçeyi Satmalı?
Mehmet Bey’in aynı büyüklükte iki portakal bahçesi vardır. Bunlardan birini satacaktır. Bu bahçelerden elde edilen portakal miktarları aşağıda verilmiştir.
1. Her iki bahçenin yılda ortalama kaç kg portakal verdiğini bulunuz.
2. Her iki veri grubunun medyanını bulunuz.
3. Her iki veri grubunun varsa tepe değerini bulunuz.
4. Nasıl bir sonuç elde ettiniz? Tartışınız.
5. Siz bu bahçelerden birini alacak olsanız, hangisini alırdınız? Neden?
6. Bu iki veri grubunu karşılaştırmak için merkezi eğilim ölçüleri yeterli mi?
Bilgi Notu : İki ya da daha çok veri grubunu karşılaştırmada, aritmetik ortalamanın yeterli olmadığı durumlarda standart sapma hesaplanır. Standart sapmanın küçük olması riskin az (dağılımın homojen), standart sapmanın büyük olması riskin çok (verilerin dağınık) olduğunun göstergesidir.
Bilgi Notu : Standart sapma hesaplanırken;
• Verilerin aritmetik ortalaması hesaplanır.
• Her bir veriden aritmetik ortalama çıkılarak bulunan sayının karesi alınır.
• Bulunan kareler toplanır.
• Toplam, veri sayısının bir eksiğine bölünür.
• Bölümün karekökü alınır.
Böylece veri grubunun standart sapması bulunmuş olur.
Örnek : Teog sınavına girecek olan Eda ve Elçim’in deneme sınavlarında yaptıkları net soru sayıları aşağıda verilmiştir.
Eda : 80, 45, 60, 75, 70, 10, 60, 90, 60, 50
Elçim : 65, 60, 60, 70, 50, 55, 60, 50, 55, 75
En son yapılacak deneme sınavında, hangisinin daha başarılı olacağını tahmin edin.
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Histogram Konu Anlatımı
Histogram
Çektiğimiz fotoğraf acaba ne kadar iyi? Bunun en hızlı cevabını histogram grafiğinden bulabiliriz. Histogram grafiği ışık dağılımını gösteren bir grafiktir.
Histogram ilk bakışta tam olarak kaçı gösterdiğinin bilincinde olmadığımız, ama zamanı yaklaşık söyleyebildiğimiz bir saat gibi, epeyce bilgi aktarır. Saat örneğine benzer bir şekilde histogramı okumada da beceri kazanmak, bir konunun fotoğrafında, seçilen ışıklama değerlerini ya da görüntünün kalitesini çabucak değerlendirebilme yeteneğini kazanmak anlamına gelir.
Histogram Oluştururken
Verileri gruplamak için uygun grup genişliği belirlenir.
Veri gruplarının sayısının 10 civarında olması uygundur.
Grafiklerde aralıklarda hiç veri olmaması nedeniyle yanlış yorumlara yol açmamak için “zikzak” kullanılmıştır.
Grafiklerde uygun ölçekler kullanılır.
Tabloya başlık yazılır.
Grafiklerin başlıkları yazılmalı ve eksenleri isimlendirilmelidir.
Histogramda Grup Genişliğini Farklı Yöntemlerle Bulma
Çeşitli kaynaklarda verilerin doğru yorumlanabilmesi için grup sayısının 10 civarında olması öneriliyor. Açıklık, 10, 11 vb istenilen grup sayısına bölünür. Bulunan sayıya en yakın büyük tek sayı grup genişliği olarak alınır.
“Açıklık/grup sayısı” işleminin sonucu örneğin “4” çıktığında en yakın tek sayılar “3” ve “5” tir. Bunlardan büyük olan “5” olduğu halde grup genişliği “5” olur.
Örneğin sonuç “3,5” olduğunda en yakın tek sayı “3” tür. O halde, en büyük değer “3” tür. Bu nedenle, grup genişliği “3” olarak alınır.
Aynı yöntemle elde edilen grup genişliği (açıklık/grup sayısı) en yakın tam sayıya yuvarlayarak da kullanılabilir. Sonuç “3,7” çıktığında en yakın tam say olan “4” grup genişliği olarak alınabilir.
Etkinlik
Fazla Sayıda Verilerle Grafik Oluşturuyorum.
Bir üniversitede “Haydi Kızlar Okula” projesine destek için yapılan ve 3 gün süren eğitim paneline konuşmacı olarak katılan kişilerin adları ve yaşları aşağıdaki tabloda verilmiştir.
| 8. Sınıf Histogram | Açıklama | Test Linki |
| 1. Histogram | 8. Sınıf Matematik Histogram Testleri | Teste Başla |
| 2. Histogram | 8. Sınıf Matematik Histogram Test | Teste Başla |
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Denklemler Konu Anlatımı
Denklemler
Saatteki hızı belli olan bir aracın iki şehir arasında kaç kilometre yol aldığı bilindiğinde yolculuğun kaç saat sürdüğü hesaplanabilir.
Aralarındaki ardışık fark bilinen sayıların toplamı verildiğinde en küçük veya en büyük sayıyı bulmak kolaydır.
a + 4 = 5 -> I. Dereceden bilinmeyenli denklem
2a – 3 = a + 4 -> I. Dereceden bir bilinmeyenli denklem
İki kardeşin yaşları toplamı ve farkı bilindiğinde yaşları bulunabilir. İki işçinin bir işi yapma süreleri verildiğinde bu işi birlikte ne kadar sürede yapılabilecekleri belirlenebilir.
Nicelikler arasında ilişkilerden yararlanarak bilinmeyen değerlere denklemler yoluyla ulaşılabilir.
X2 – 2x – 3 = 0 -> II. dereceden bir bilinmeyenli denklem
X + 4y = 5 -> I. Dereceden iki bilinmeyenli denklem
Birinci Dereceden Bir Bilinmeyenli Denklem : a, b ∈ R ve a≠0 olmak üzere ax+b = 0 biçimindeki denklemdir.
Denklemin Kökü : Denklemi sağlayan değerlerdir.
Denklemin Çözümü : Denklemin kökünü bulmak için yapılan işlemlerdir.
Çözüm (Doğruluk) Kümesi : Elemanları denklemin kökleri olan kümedir. Ç ile gösterilir.
Denklem Çözümlerinde Bilinmesi Gereken Özellikler
- a, b, c ∈ R ve c ≠ 0 olmak üzere eşitliğin her iki tarafında aynı sayı eklenir veya çıkarılırsa eşitlik bozulmaz.
A + c = b + c
A – c = b – c
- Eşitliğin her iki tarafı aynı sayı ile çarpılır veya bölünürse eşitlik bozulmaz.
A . c = b . c
A : c = b : c
- Bir denklemde herhangi bir t erim, eşitliğin bir tarafından diğer tarafına geçilirken işaret değiştirir.
| 8. Sınıf Denklemler | Açıklama | Test Linki |
| 1. Denklemler | 8. Sınıf Matematik Denklemler Testleri | Teste Başla |
| 2. Denklemler | 8. Sınıf Matematik Denklemler Test | Teste Başla |
| 3. Denklemler | 8. Sınıf Matematik Denklemler Testi | Teste Başla |
| 4. Denklemler | 8. Sınıf Matematik Denklemler Online Test | Teste Başla |
| 5. Denklemler | 8. Sınıf Matematik Denklemler Test Çöz | Teste Başla |
| 6. Denklemler | 8. Sınıf Matematik Denklemler Problemleri | Teste Başla |
| 7. Denklemler | 8. Sınıf Matematik Denklemler Soruları | Teste Başla |
| 8. Denklemler | 8. Sınıf Denklemler İle İlgili Sorular | Teste Başla |
| 9. Denklemler | 8. Sınıf Denklemler İle İlgili Test Çöz | Teste Başla |
| 10. Denklemler | 8. Sınıf Denklemler Soru Çöz | Teste Başla |
| 11. Denklemler | 8. Sınıf Denklemler Genel Değerlendirme | Teste Başla |
| 12. Denklemler | 8. Sınıf Denklemler Konu Tarama | Teste Başla |
| 13. Denklemler | 8. Sınıf Denklemler Konu Tarama 2 | Teste Başla |
| 14. Denklemler | 8. Sınıf Denklemler Konu Tarama 3 | Teste Başla |
| 15. Denklemler | 8. Sınıf Denklemler Konu Tarama 4 | Teste Başla |
| 16. Denklemler | 8. Sınıf Denklemler Deneme Sınavı | Teste Başla |
| 17. Denklemler | 8. Sınıf Denklemler Deneme Sınavı 2 | Teste Başla |
Kategoriler: Matematik Etiketler: