8. Sınıf Matematik Üçgenlerde Eşlik Benzerlik Konu Anlatımı
Üçgenlerde Eşlik ve Benzerlik
Eş ve Benzer Şekiller
Çevremizde eş ve benzer olan birçok nesneyle karşılaşabiliriz. Küpeyi oluşturan parçaların görünümleri ve büyüklükleri aynı olduğundan birbirinin eşidir. Tatlı ve çorba kaşıkları ise görünümleri aynı, büyüklükleri farklı olduğundan birbirine benzerdir. Bir şekli veya bir resmi belli bir oranda büyüterek veya küçülterek benzer şekiller, resimler elde edilir.
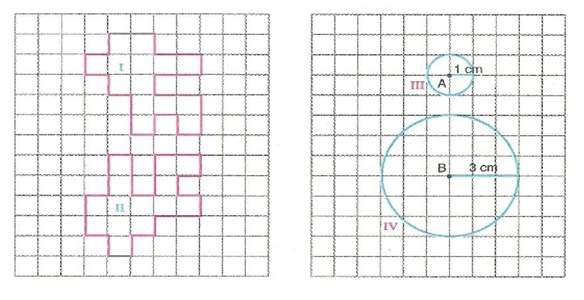
- şekil, I. Şeklin saat yönünün tersinde 90° döndürülmesiyle elde edildiğinden şekillerin biçimleri ve büyüklükleri aynıdır.
I ≅ II veya II ≅ I yazılabilir.
A merkezli çemberin yarıçapı 3 katına çıkarılarak B merkezli çember elde edildiğinden çemberlerin biçimleri aynı, büyüklükleri farklıdır.
III ∼ IV veya IV ∼ III yazılabilir.
Eş şekillerin benzerlik oranı 1 olduğundan I ve II nolu şekillerin kenarlarının oranı 1’dir. A ve B merkezli benzer çemberlerin yarıçapları oranı 1/3 olduğundan benzerlik oranı 1/3’tür. Benzer şekillerin kenar uzunlukları oranına benzerlik oranı denir. Bu oran “k” sembolü ile gösterilir. (k ∈ R+)
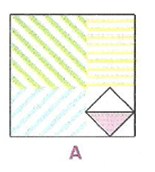
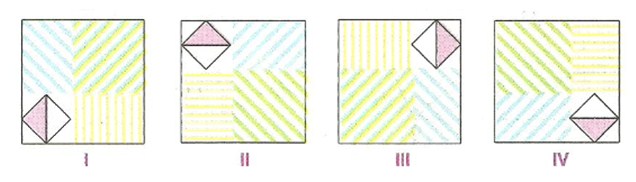
A şeklinin döndürülmesiyle oluşan şekillerin her biri A şeklinin ve birbirinin eşidir.
A şeklinin saat yönünde 90, 180, 270, 360 derece döndürülmesiyle sırasıyla I, II, III ve IV. şekiller oluşur.
Eş ve Benzer Şekilleri Okuma :
A ve B şekilleri eş ise “A eştir B”. Veya “A, B’ye eştir.” biçiminde okunur ve “A ≅ B” ile gösterilir.
A ve B şekilleri benzer ise “A benzerdir B.” veya “A, B’ye benzerdir.” biçiminde okunur ve “A ∼ B” ile gösterilir.
| 8. Sınıf Üçgenlerde Eşlik ve Benzerlik | Açıklama | Test Linki |
| 1. Üçgenlerde Eşlik ve Benzerlik | 8. Sınıf Matematik Üçgenlerde Eşlik ve Benzerlik Testleri | Teste Başla |
| 2. Üçgenlerde Eşlik ve Benzerlik | 8. Sınıf Matematik Üçgenlerde Eşlik ve Benzerlik Test | Teste Başla |
| 3. Üçgenlerde Eşlik ve Benzerlik | 8. Sınıf Matematik Üçgenlerde Eşlik ve Benzerlik Testi | Teste Başla |
| 4. Üçgenlerde Eşlik ve Benzerlik | 8. Sınıf Matematik Üçgenlerde Eşlik ve Benzerlik Online Test | Teste Başla |
| 5. Üçgenlerde Eşlik ve Benzerlik | 8. Sınıf Matematik Üçgenlerde Eşlik ve Benzerlik Test Çöz | Teste Başla |
| 6. Üçgenlerde Eşlik ve Benzerlik | 8. Sınıf Matematik Üçgenlerde Eşlik ve Benzerlik Problemleri | Teste Başla |
| 7. Üçgenlerde Eşlik ve Benzerlik | 8. Sınıf Matematik Üçgenlerde Eşlik ve Benzerlik Soruları | Teste Başla |
| 8. Üçgenlerde Eşlik ve Benzerlik | 8. Sınıf Üçgenlerde Eşlik ve Benzerlik İle İlgili Sorular | Teste Başla |
| 9. Üçgenlerde Eşlik ve Benzerlik | 8. Sınıf Üçgenlerde Eşlik ve Benzerlik İle İlgili Test Çöz | Teste Başla |
| 10. Üçgenlerde Eşlik ve Benzerlik | 8. Sınıf Üçgenlerde Eşlik ve Benzerlik Soru Çöz | Teste Başla |
| 11. Üçgenlerde Eşlik ve Benzerlik | 8. Sınıf Üçgenlerde Eşlik ve Benzerlik Genel Değerlendirme | Teste Başla |
| 12. Üçgenlerde Eşlik ve Benzerlik | 8. Sınıf Üçgenlerde Eşlik ve Benzerlik Konu Tarama | Teste Başla |
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Üçgenlerde Kenar Açı İlişkileri Konu Anlatımı
Üçgenlerde Kenar Açı İlişkileri
Üçgenlerde Kenar Açı İlişkileri
Üçgenlerin kenarlarıyla açıları arasında bazı bağıntıları bulunmaktadır. Nasıl üçgenlerin iç açıları toplamı 180°’yi geçemediğinden açılar her istenilen değeri alamıyorsa, kenar uzunlukları da her istenilen değeri alamaz. Bunun için kenar uzunlukları arasındaki ilişkiyi bilmek gerekir.
Üçgen Eşitsizliği
Üçgende a, b ve c kenar uzunluklarının alabileceği değerleri bulmak için yazılan üçgen eşitsizlikleri,
|b-c| < a < b + c
|a-c| < b < a + c
|a-b| < c < a + b
Örnek 1 :

ABC üçgeninde |BC|’nun alabileceği kaç tam sayı değeri vardır?
7 – 5 < |BC| < 7 + 5
2 < |BC| < 12
|BC|’nun alabileceği tam sayı değerleri 3, 4, 5, 6, 7, 8, 9, 10, 11 olup 9 tanedir.
Örnek 2 :

7 – 6 < |AB| < 7 + 6
1 < |AB| < 13 ve
|AB| < |BC|’ndan |AB| < 7’dir.
1 < |AB| < 7 olduğuna göre
2 + 3 + 4 + 5 + 6 = 20 cm’dir.
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Üçgenlerde Kenarlar ve Açılar Konu Anlatımı
Üçgende Kenarlar ve Açılar
Üçgen ve Özellikleri
Günlük hayatta birçok yerde üçgen şekline rastlayabiliriz. Bir kara parçası, bir çadır, bir saat ve daha fazlası üçgen biçiminde olabilir.
Matematikte en çok karşımıza çıkan geometrik şekil üçgendir. Çokgenler içinde kenar sayısı en az olan üçgenler, diğer çokgenlerle ilgili özellikleri de ortaya çıkarmaya yarar.
Üçgende Açılar
Bir ABC üçgeninin iç açılarının ölçüleri toplamı 180° dir.
x + y + z = 180°
Bir ABC üçgeninin dış açılarının ölçüleri toplamı 360° dir.
180° – x + 180° – y + 180° – z
= 540° – (x+y+z)
= 540° – 180° = 360°
Bir ABC üçgeninde bir dış açı ile bir iç açının ölçüsü toplamı 180° dir.
x + y = 180°
Bir ABC üçgeninin bir dış açısının ölçüsü, kendisine komşu olmayan iki iç açısın ölçüleri toplamına eşittir.
[AD // [BC], [BE // [CA],
[CF // [AB]’dır.
Örnek 1 : Bir KLM üçgeninin iç açılarının ölçüleri sırasıyla 3, 5 ve 7 ile orantılıdır. Buna göre en küçük açının ölçüsü kaç derecedir?
Çözümü :
Açılar 3x, 5x, 7x olarak yazılırsa
3x + 5x + 7x = 180°
15x = 180°
X = 12° bulunur.
En küçük açı
3x = 3 . 12° = 36° dir.
| 8. Sınıf Üçgenlerde Kenarlar ve Açılar | Açıklama | Test Linki |
| 1. Üçgenlerde Kenarlar ve Açılar | 8. Sınıf Matematik Üçgenlerde Kenarlar ve Açılar Testleri | Teste Başla |
| 2. Üçgenlerde Kenarlar ve Açılar | 8. Sınıf Matematik Üçgenlerde Kenarlar ve Açılar Test | Teste Başla |
| 3. Üçgenlerde Kenarlar ve Açılar | 8. Sınıf Matematik Üçgenlerde Kenarlar ve Açılar Testi | Teste Başla |
| 4. Üçgenlerde Kenarlar ve Açılar | 8. Sınıf Matematik Üçgenlerde Kenarlar ve Açılar Online Test | Teste Başla |
| 5. Üçgenlerde Kenarlar ve Açılar | 8. Sınıf Matematik Üçgenlerde Kenarlar ve Açılar Test Çöz | Teste Başla |
| 6. Üçgenlerde Kenarlar ve Açılar | 8. Sınıf Matematik Üçgenlerde Kenarlar ve Açılar Soruları | Teste Başla |
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Çarpanlara Ayırma Konu Anlatımı
Çarpanlara Ayırma
Sayılarda olduğu gibi cebirsel ifadelerin de iki veya daha fazla terimin çarpımı biçiminde yazılmasıdır.
Çarpan ağacı, sayıları çarpanlarına ayırmada kullanılan bir yöntemdir. Bu yöntemle sayılar asal çarpanlarına da ayrılabilir.
36 = 4.9 = 22.32 eşitliğinde 4 ve 9 sayıları çarpan, 2 ve 3 sayıları asal çarpandır. Cebirsel ifadeler de benzer şekilde çarpanlarına ayrılabilir.
Ortak Çarpan Parantezine Alma
Bir cebirsel ifadeyi ortak çarpan parantezine almanın amacı terim sayısını azaltmaktır. Böylece özellikle rasyonel cebirsel ifadelerde sadeleştirmeler yapılır, işlem daha sadece hale getirilir. Bir cebirsel ifadede ortak çarpan belirlendikten sonra parantez içi, çarpanlarına ayrılan ifadenin her teriminin ortak çarpana bölünmesiyle elde edilir.
Gruplandırarak Çarpanlara Ayırma
Bazı cebirsel ifadelerde terimlerin tümünü bölen bir ortak çarpan olmayabilir. Bu durumda terimler kendi aralarında ortak çarpanı olacak şekilde ikişerli, üçerli gruplara ayrılır. Bu gruplar çarpanlarına ayrılır, eğer ortak çarpan varsa ortak çarpan parantezine alınır. Çarpanlara ayırma işlemi tamamlanmış olur.
6ab + 8a – 9b – 12 ifadesinde tüm terimler için ortak çarpan yoktur. 6ab + 8a – 9b – 12 biçiminde gruplandırılırsa
6ab + 8a = 2a . (3b + 4)
9b + 12 = 3 . (3b + 4) yazılabilir.
2a . (3b + 4) – 3 . (3b + 4) ifadesinde ortak çarpan 3b + 4 ‘tür.
(3b + 4) . (2a – 3)
Örnek : x2 – y2 + 9 + 6x ifadesinin çarpanları nelerdir?
İfade x2 + 6x + 9 – y2 biçiminde düzenlenirse,
x2 + 6x + 9 – y2 = (x + 3) 2 – y2
= (x + 3 + y) . (x + 3 – y) çarpanlarına ayrılır.
| 8. Sınıf Çarpanlara Ayırma | Açıklama | Test Linki |
| 1. Çarpanlara Ayırma | 8. Sınıf Matematik Çarpanlara Ayırma Testleri | Teste Başla |
| 2. Çarpanlara Ayırma | 8. Sınıf Matematik Çarpanlara Ayırma Test | Teste Başla |
| 3. Çarpanlara Ayırma | 8. Sınıf Matematik Çarpanlara Ayırma Testi | Teste Başla |
| 4. Çarpanlara Ayırma | 8. Sınıf Matematik Çarpanlara Ayırma Online Test | Teste Başla |
| 5. Çarpanlara Ayırma | 8. Sınıf Matematik Çarpanlara Ayırma Test Çöz | Teste Başla |
| 6. Çarpanlara Ayırma | 8. Sınıf Matematik Çarpanlara Ayırma Problemleri | Teste Başla |
| 7. Çarpanlara Ayırma | 8. Sınıf Matematik Çarpanlara Ayırma Soruları | Teste Başla |
| 8. Çarpanlara Ayırma | 8. Sınıf Çarpanlara Ayırma Genel Değerlendirme | Teste Başla |
| 9. Çarpanlara Ayırma | 8. Sınıf Çarpanlara Ayırma Konu Tarama | Teste Başla |
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Özdeşlikler Konu Anlatımı
Özdeşlikler
Özdeşlik : İçindeki değişkenin her değeri için doğru olan önermelerdir.
Denklem : İçinde en az bir değişken bulunan ve değişkenin bazı özel değerleri için doğru olan önermelerdir.
3a. (a + 1) = 3a2 + 3a açık önermesinde a yerine hangi değerler yazılırsa eşitlik sağlanır.
A yerine farklı sayılar yazmaya devam edilerek de eşitliğin daima sağlandığı gösterilebilir.
2x + 7 = 9 önermesinde x yerine hangi değerler yazılırsa eşitlik olur.
X yerine 1’den farklı sayılar yazıldığında eşitlik sağlanmaz.
Eşitliği sağlayan tek değer x = 1’dir.
| 8. Sınıf Özdeşlikler | Açıklama | Test Linki |
| 1. Özdeşlikler | 8. Sınıf Matematik Özdeşlikler Testleri | Teste Başla |
| 2. Özdeşlikler | 8. Sınıf Matematik Özdeşlikler Test | Teste Başla |
| 3. Özdeşlikler | 8. Sınıf Matematik Özdeşlikler Testi | Teste Başla |
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik İrrasyonel Sayılar ve Eşitsizlikler Konu Anlatımı
İrrasyonel Sayılar
1. Her rasyonel sayının sayı doğrusu üzerinde eşleştiği bir nokta vardır.
2. Sayı doğrusu üzerinde ![]() , … gibi rasyonel sayılarla eşleşmeyen bazı noktalar vardır. Bu noktaların eşleştiği sayılara, irrasyonel sayılar denir. İrrasyonel sayılar, İ ile gösterilir.
, … gibi rasyonel sayılarla eşleşmeyen bazı noktalar vardır. Bu noktaların eşleştiği sayılara, irrasyonel sayılar denir. İrrasyonel sayılar, İ ile gösterilir.
3.İrrasyonel sayılar a/b (a, b ∈ Z ve b ≠ 0) biçiminde yazılamaz.
4. İrrasyonel sayılarla rasyonel sayıların birleşim kümesine, gerçek (reel) sayılar kümesi denir. Reel sayılar kümesi R ile gösterilir.
İ ∩ Q =∅, İ ∪ Q = R dir.
Reel sayılar kümesinin şema ile gösterimi;
Eşitsizlikler
Eşitlik ve eşitsizlik durumları denge modeli kullanılarak incelenebilir.

Eşitlik, dengede olma durumu olarak ifade edilir.
Eşitsizlik, dengede olmama durumu olarak ifade edilir.
Eşitsizilk : >(büyük), <(küçük), ≥(büyük eşit), ≤(küçük eşit) sembolleriyle ifade edilen açık önermelerdir.
Pratik Bilgiler
- a.b>O ise a ile b aynı işaretli,
- a.b<O ise a ile b zıt işaretli,
- a <|a| ise a<O,
- a2<a ise O<a<1’dir.
Adaletin Eşitliği
Adalet, haklılık ve hakka uygunluktur. Haklı ve haksızın ayırt edilmesi adaletle sağlanır. Öznel anlamda adalet herkesin hakkını tanıma konusunda değişmez ve kesin istektir. Nesnel anlamda ise karşıt çıkarlar arasında hukuka uygun bir denkliktir. Adalet, eşitlik düşüncesidir.
Düşünürler eski çağlardan beri adalet kavramıyla ilgilenmişlerdir. Kutsal kitapların hepsinde adalete ve adil olmaya ilişkin bölümler bulunur. Eski Yunanlı düşünür Platon’a göre adalet en yüce erdemlerden biri olup insanın ve devletin temel davranış kuralıdır. Aristonun hareket noktasını ise eşitlik kavramı oluşturur. Ona göre herkese eşit davranmak adalet için yeterli değildir. Bir hukuk düzeni güçsüzleri koruduğu ölçüde başarılı olabilir. Örneğin, kişinin tükettiği herhangi bir madlen alınan katma değer vergisi adil bir vergi değildir. Çünkü kişinin gelir düzeyi dikkate alınmaz. Kişinin geliri üzerinden alınan ve gelir düzeyi yükseldikçe vergi oranının arttığı gelir vergisi ise daha adildir.
Günümüzdeki adalet kavramı sosyal adaleti de kapsamaktadır. Sosyal adalet, ekonomik, sosyal ve kültürel değerlerin dağılımındaki dengesizliklerin giderilmesini, toplumda yardıma muhtaç olanların devletçe desteklenmesini amaçlar.
| 8. Sınıf İrrasyonel Sayılar ve Eşitsizlikler | Açıklama | Test Linki |
| 1. İrrasyonel Sayılar ve Eşitsizlikler | 8. Sınıf Matematik İrrasyonel Sayılar ve Eşitsizlikler Testleri | Teste Başla |
| 2. İrrasyonel Sayılar ve Eşitsizlikler | 8. Sınıf Matematik İrrasyonel Sayılar ve Eşitsizlikler Test | Teste Başla |
| 3. İrrasyonel Sayılar ve Eşitsizlikler | 8. Sınıf Matematik İrrasyonel Sayılar ve Eşitsizlikler Testi | Teste Başla |
| 4. İrrasyonel Sayılar ve Eşitsizlikler | 8. Sınıf Matematik İrrasyonel Sayılar ve Eşitsizlikler Online Test | Teste Başla |
| 5. İrrasyonel Sayılar ve Eşitsizlikler | 8. Sınıf Matematik İrrasyonel Sayılar ve Eşitsizlikler Test Çöz | Teste Başla |
| 6. İrrasyonel Sayılar ve Eşitsizlikler | 8. Sınıf Matematik İrrasyonel Sayılar ve Eşitsizlikler Problemleri | Teste Başla |
| 7. İrrasyonel Sayılar ve Eşitsizlikler | 8. Sınıf Matematik İrrasyonel Sayılar ve Eşitsizlikler Soruları | Teste Başla |
| 8. İrrasyonel Sayılar ve Eşitsizlikler | 8. Sınıf İrrasyonel Sayılar ve Eşitsizlikler İle İlgili Sorular | Teste Başla |
| 9. İrrasyonel Sayılar ve Eşitsizlikler | 8. Sınıf İrrasyonel Sayılar ve Eşitsizlikler İle İlgili Test Çöz | Teste Başla |
| 10. İrrasyonel Sayılar ve Eşitsizlikler | 8. Sınıf İrrasyonel Sayılar ve Eşitsizlikler Soru Çöz | Teste Başla |
| 11. İrrasyonel Sayılar ve Eşitsizlikler | 8. Sınıf İrrasyonel Sayılar ve Eşitsizlikler Genel Değerlendirme | Teste Başla |
| 12. İrrasyonel Sayılar ve Eşitsizlikler | 8. Sınıf İrrasyonel Sayılar ve Eşitsizlikler Konu Tarama | Teste Başla |
| 13. İrrasyonel Sayılar ve Eşitsizlikler | 8. Sınıf İrrasyonel Sayılar ve Eşitsizlikler Konu Tarama 2 | Teste Başla |
| 14. İrrasyonel Sayılar ve Eşitsizlikler | 8. Sınıf İrrasyonel Sayılar ve Eşitsizlikler Konu Tarama 3 | Teste Başla |
| 15. İrrasyonel Sayılar ve Eşitsizlikler | 8. Sınıf İrrasyonel Sayılar ve Eşitsizlikler Konu Tarama 3 | Teste Başla |
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Kareköklü Sayılarla Çarpma Bölme Konu Anlatımı
Kareköklü Sayılarla Çarpma
Kareköklü sayılarla çarpma işlemi yapılırken, kat sayılar çarpılır ve çarpım kat sayı olarak yazılır; kök içindeki sayılar çarpılır ve çarpım kök içine yazılır.
Örnek : Kısa kenarının uzunluğu kök 5 m, uzun kenarının uzunluğu 2 kök 5 m olan dikdörtgen şeklindeki bir odanın taban alanı kaç metre karedir?
Kareköklü Sayılarla Bölme
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Kareköklü Sayılarla Toplama Çıkarma Konu Anlatımı
Kareköklü Sayılarla Toplama ve Çıkarma
Kenar uzunlukları kareköklü sayılar olarak verilen bir yamuğun çevresi hesaplanmak istenildiğinde
ABCD yamuğunun çevresini bulmak için kenar uzunlukları toplanır.
Toplama işlemini yapmak için kök içleri aynı olan terimlerin kat sayıları toplanır.
Köklü Toplama ve Çıkarma :
Kareköklü sayılarla toplama veya çıkarma işlemini yapabilmek için, terimlerin kök içlerindeki sayılar aynı olmalıdır. Kök içlerindeki sayılar aynı olmazsa toplama veya çıkarma işlemi yapılamaz.
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Kareköklü Sayılar Konu Anlatımı
Kareköklü Sayılar
Kareköklü sayılarla matematikteki işlemler dışında birçok yerde karşılaşmaktayız. Mühendislikte formül hesaplamalarında, hassas hesaplamalarda köklü sayılarla karşılaşılır. Örneğin, bir köprünün taşıyacağı yük miktarının hesabı yapılırken sonuç köklü bir sayı çıkabilir. Alanı verilen kare şeklindeki bir bahçenin kenar uzunluğunu bulmak için karekökü bulunur. Alanı 25 m2 olan bahçenin bir kenar uzunluğu ise;
Kare şeklindeki bir havuzun alanı 16 m2 dir.
Bu havuzun bir kenar uzunluğu kaç metredir?
Kare şeklindeki alanı 16 m2 olan havuzun bir kenar uzunluğunu bulmak için karekökü bulunur.
Kendisi ile çarpıldığında 25 ve 18 olan başka sayı var mıdır?
(-5) 2 = 25
(-4) 2 = 16
Karesel Sayılar :
1, 4, 9, 16, … gibi bir doğal sayının karesi olan sayılara karesel sayılar (tam kare sayılar) denir.
Tam Kare Olmayan Sayıların Karekökleri ve İrrasyonel Sayılar
X2 = 3 eşitliğini sağlayan bir tamsayı yoktur. Fakat bu eşitliği sağlayan bir sayı vardır. Tam kare olmayan sayıların karekökleri tahmin edilirken bilinen tam kare sayıların kareköklerinden yararlanılır.
3’e en yakın tam kare sayılar 1 ve 9’dur.
Bu sayılar küçükten büyüğe doğru sıralanır.
1 < 3 < 9
Karekökleri alınır.
Sonuç 1 ile 3 arasındadır.
En yakın onda birliğe kadar sayının değerini tahmin etmek için 3’ün 1 ve 9 sayılarına olan uzaklığı düşünülür.
3 – 1 = 2 ve 9 – 3 = 6’dır.
3 sayısı 1’e 9’dan daha yakın olduğundan değeri 1,7 ile 1,8 arasındadır.
Rasyonel Olmayan Sayılar :
Ünlü Matematikçi Pisagor, dünyayı tam sayılarla ve onların birbirine oranıyla yani kesirlerle açıklayabileceğinden emindi. Ancak öğrencisi Hippasus karekök 2’nin rasyonel bir sayı olamayacağını ispatladı.
Söylenenlere göre Pisagor öğrencisi Hippasus’u öldürtmüştü.
Karekök Alma
Karekök alırken üslü sayılar ve özelliklerden yararlanılır. Karekök alma, bir sayının kök işareti içinde değerini buluğ yazmaktır. Karekökü alınacak sayının kuvveti 2’nin katı şeklinde olduğunda kök dışında rasyonel bir sayı olarak çıkar. Kuvveti 2’nin katı şeklinde olmayan sayılar kök dışına rasyonel bir sayı olarak çıkamaz.
Kökün içinde bir sayı varsa bu sayının kuvveti ikiye bölünerek kök dışında çıkar. Kökün içinde çarpım veya bölüm durumunda sayılar varsa bu sayıların kuvvetleri ayrı ayrı ikiye bölünerek kök dışına çıkar.
Çok basamaklı sayıların karekökü alınırken aşağıdaki yöntem uygulanabilir.
Sonra, 8’in karekökü bulunur. 8’in karekökü yaklaşık 2’dir. 2 = 4 sayısı 8’in altına yazılarak çıkarma işlemi yapılır.
Daha sonra, kalan 4’ün yanına 41 yazılır. Bulunan 2 sayısının 2 katı alınır. 2 x 2 = 4 sayısının sağına hangi sayı yazılıp bu sayı ile çarpılırsa 441 olacağı bulunur. Bu sayı 9’dur.
Bulunan 9 sayısı, daha önce bulunan 2’nin sağına yazılarak iki basamaklı 29 sayısı elde edilir. 841 sayısının karekökü 29’dur.
Alanı 12 m2 olan kare şeklindeki bahçenin bir kenar uzunluğu kaç metredir?
12, tam kare bir sayı değildir. 12’nin karekökü bulunurken sayı asal çarpanlara ayrılır.
| 8. Sınıf Kareköklü Sayılar | Açıklama | Test Linki |
| 1. Kareköklü Sayılar | 8. Sınıf Matematik Kareköklü Sayılar Testleri | Teste Başla |
| 2. Kareköklü Sayılar | 8. Sınıf Matematik Kareköklü Sayılar Test | Teste Başla |
| 3. Kareköklü Sayılar | 8. Sınıf Matematik Kareköklü Sayılar Testi | Teste Başla |
| 4. Kareköklü Sayılar | 8. Sınıf Matematik Kareköklü Sayılar Online Test | Teste Başla |
| 5. Kareköklü Sayılar | 8. Sınıf Matematik Kareköklü Sayılar Test Çöz | Teste Başla |
| 6. Kareköklü Sayılar | 8. Sınıf Matematik Kareköklü Sayılar Problemleri | Teste Başla |
| 7. Kareköklü Sayılar | 8. Sınıf Matematik Kareköklü Sayılar Genel Değerlendirme | Teste Başla |
| 8. Kareköklü Sayılar | 8. Sınıf Kareköklü Sayılar Konu Tarama | Teste Başla |
Kategoriler: Matematik Etiketler:
8. Sınıf Matematik Gerçek Sayılar Konu Anlatımı
Gerçek Sayılar
Matematikte şimdiye kadar kullandığımız sayıları düşünün. Bu sayıları düşünün. Bu sayıların hepsini içine alan bir sayı kümesi var mıdır? İşte bu sayı kümesi, gerçek (reel) sayılar kümesidir.
Gerçek (Reel) sayılar kümesi R ile gösterilir.
Pozitif gerçek sayılar kümesi R+, negatif gerçek sayılar kümesi R- ile gösterilir.
Reel Sayılar Kümesi :
Rasyonel sayılar kümesi ile irrasyonel sayılar kümesinin birleşim kümesidir.
Pozitif Reel Sayılar Kümesi :
0’dan büyük gerçek sayılar kümesidir.
Negatif Reel Sayılar Kümesi :
0’dan küçük gerçek sayılar kümesidir.
Kategoriler: Matematik Etiketler: