7. Sınıf Matematik Çokgenler Konu Anlatımı
Çokgenler
Doğrusal olmayan en az üç noktanın birleştirilmesiyle oluşan kapalı geometrik şekillere çokgen denir. Çokgenler kenar sayılarına göre isimlendirilir. N kenarlı bir çokgen “n – gen” olarak isimlendirilir. Çokgen üç kenarlı ise üçgen, dört kenarlı ise dörtgen, beş kenarlı ise beşgen, altı kenarlı ise altıgen ……. olarak isimlendirilir.
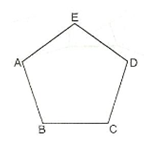
Şekildeki çokgende, A, B, C, D, E çokgenin köşeler; [AB], [BC], [CD], [DE] ve [EA] çokgenin kenarlarıdır. A, B, C, D, E köşelerine ait çokgenin iç bölgesinde kalan açılar çokgenin iç açılarını oluşturur.
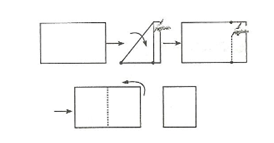
Bir kağıt kısa kenarı bir komşu uzun kenar üzerine gelecek şekilde katlanır ve uzun kenarlar üzerine gelen noktalar işaretlenir. Kağıt bu noktalardan kendi üzerine gelecek şekilde yeniden katlanırsa bir “kare” modeli oluşur.
Kağıt yardımıyla ikişer ikişer kesişen ve birbirine paralel olmayan üç kat çizgisi ile bir “üçgen” modeli oluşturulur.
Uzun bir kağıt şerit düğüm atılarak iki ucundan çekilerek düzlenir. Yandan artan fazla parçalar kesilerek beşgen oluşturulur.
Kağıttan iki uzun şerit kesilerek şeritler şekildeki gibi katlanarak karşılıklı yerleştirilir ve iki yandan çekilerek düzlenirse fazla parçalar kesildiğinde ortada “altıgen” modeli oluşturulur.
Tüm kenar uzunlukları ve iç açılarının ölçüleri eşit olan çokgenlere düzgün çokgen denir.
Örnek : n tane kenarı olan bir çokgenin bir köşesinden n – 3 tane köşegen çizilir.
Altıgenin bir köşesinden kaç tane köşegen çizilir?
Çözüm : n = 6 -> n – 3 = 6 – 3 = 3 tanedir.
Örnek : n tane kenarı olan bir çokgenin aynı köşesinden çizilen köşegenler n – 2 tane üçgen oluşturur.
Altıgenin bir köşesinden çizilen köşegenlere altıgenin içinde kaç tane üçgen oluştur?
Çözüm : n = 6 -> n – 2 = 6 – 2 = 4 tane üçgen oluşur.
N tane kenarı olan çokgenin iç açıları toplamı 180.(n-2)’dir.
Yedigende x ile gösterilen açının ölçüsünü bulalım.
Çözüm : n = 7 -> iç açıları toplamı 180.(7-2) = 180 . 5 = 900°
Çokgenin verilen iç açıları toplamı = 130 + 115 + 140 + 120 + 135 + 160 = 800°
Verilmeyen açı 900 – 800 = 100°’dir.
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik Doğrular ve Açılar Konu Anlatımı
Doğrular ve Açılar
A. Düzlemde Doğrular
1. Bir noktanın bir doğruya olan en kısa uzaklığı
Bir noktanın bir doğruya olan en kısa uzaklığı, bu noktadan doğruya çizilen dikmenin uzunluğudur.
Yukarıdaki şekilde [TC] ⊥ d olduğundan T noktasının d doğrusuna en kısa uzaklığı |TC| dir.
2. Bir doğru parçasının orta dikmesi
Bir doğru parçasının orta dikmesi, bu doğru parçasını iki eş parçaya ayırır. Ayrıca orta dikme üzerindeki noktaların doğru parçasının uç noktalarına olan uzaklıkları birbirine eşittir.
Yukarıdaki şekilde [KC] ⊥ [AB] ve |AC| = |CB| olduğundan |TA| = |TB| ve |KA| =|KB| dir.
3. Bir Düzlemde İki Doğrunun Birbirine Göre Durumları
Çakışık Doğrular :
Aynı düzlemde ve aynı iki noktadan geçen doğrulara çakışık doğrular denir.
Kesişen Doğrular :
Aynı düzlemde yalnız bir ortak noktası bulunan doğrulara kesişen doğrular denir.
Dik Doğrular :
Aynı düzlem üzerinde bulup, birbirini dik olarak kesen doğrulardır.
Paralel Doğrular :
Aynı düzlem üzerinde bulunan ve birbirlerini hiç kesmeyen, ortak noktası bulunmayan doğrulardır.
4. Bir Düzlemde Farklı Üç Doğrunun Birbirine Göre Durumları
Bir düzlemde bulunan üç farklı doğru birbirine göre dört farklı durumda bulunurlar.
Bu durumlar,
b, d ve e doğruları bir A noktasında kesişirler.
m ile n paralel, d doğrusu ise bu iki doğruyu, farklı iki noktadan kesmektedir.
üç doğru birbirini üç farklı noktada keserler.
d, k ve n doğruları paraleldir.
B. Paralel İki Doğrunun Bir Kesenle Yaptığı Açılar
Paralel iki doğruyu üçüncü bir doğrunun kesmesiyle oluşan açılardır.
1. Yöndeş Açılar :
Paralel iki doğruyu üçüncü bir doğrunun kesmesiyle oluşan açılardan aynı yöne bakan açılara yöndeş açılar denir.
Şekilde ;
Yöndeş açıların ölçüleri birbirine eşittir.
2. İç Ters Açılar
Şekildeki
İç ters açılarının ölçüleri birbirine eşittir.
3. Dış Ters Açılar
Şekilde;
Dış ters açılarının ölçüleri birbirine eşittir.
4. Karşı Durumlu Açılar
Şekilde;
Karşı durumlu açılar bütünler açılardır.
Özel Durumlar
Şekilde; b = a+c’dir.
Şekilde görüldüğü gibi B köşesinden d ve d doğrularına paralel d doğrusu çizersek iç ters açılar oluşur. b = a + c olduğu görülür.
Paralel çizgiler arasında zikzak çizildiğinde, bir tarafa bakan açıların ölçüleri toplamı diğer tarafa bakan açıların ölçüleri toplamına eşittir.
a + b + c = x + y
[AB // [DE ise;
a + b + c = 360° dir.
[AB ve [DE ye paralel [CF çizilirse iç ters açılardan a + b + c = 360° bulunur.
Kategoriler: Matematik Etiketler:
7.Sınıf Matematik Yüzde Hesaplamaları Konu Anlatımı
Yüzde Hesaplamaları
Ondalık Kesirleri Yüzde Sembolü İle Gösterme
Ondalık sayı önce kesir şeklinde yazılır. Paydası 100 olacak şekilde pay ve paya aynı sayma sayısı ile genişletilir. Böylece ilk kesre denk bir kesir elde edilmiş olur. Oluşan bu kesir yüzde sembolü kullanılarak yazılır.
Örnek : 2/5 kesrini yüzde sembolü ile gösterelim.
Çözüm : 2/5 kesrini yüzde sembolü ile gösterirken denk kesirlerden yararlanabiliriz.
Örnek : 1,16 kesrini yüzlük kartlarla modelleyerek yüzdeye çeviriniz.
Yüzde Sembolüyle Verilen İfadenin Ondalık Kesir Şeklinde Yazılması
Örnek : %17 sayısının ondalık kesir olarak yazılışını bulunuz.
Sonuç olarak her yüzdelik ifade bir kesir ya da ondalık sayı olarak yazılabilir.
Not : Bir ondalık kesrin paydası 100 ise sembol ile kolayca gösterebiliriz. Ondalık kesrin paydası 100 değil ise pay ve paydası, paydası, paydayı 100 yapacak olan sayma sayısı ile çarpılır.
Eğer paydayı 100 yapacak bir sayma sayısı bulunamıyorsa pay paydaya bölünerek kesri ondalık sayı şeklinde yazmaya çalışırız.
Kesrin ondalık açılımını yazıp virgülü iki basamak sağa kaydırır ve yüzde sembolü kullanarak yazabiliriz.
Şimdi bu son durumu bir örnekle pekiştirelim.
Örnek : 2/3 kesrini yüzde sembolü kullanarak gösteriniz.
Yüzde İfadelerinin Karşılaştırılması
Yüzdelik sayıları karşılaştırırken iki yöntem kullanabiliriz.
- Yüzdelik kısmı büyük olan yüzde sayısı büyüktür.
Örneğin %50 ile %55 sayısını karşılaştıralım.
Yüzdelik kısımlarına bakarsak
50 ve 55’i 50 < 55 şeklinde sıralayabiliriz.
Dolayısıyla %50 < %55 olur.
Ya da
- Yüzdelik sayıyı kesir sayısına çevirerek sıralayabiliriz.
Örneğin; %32 ile %62 yüzdelik sayılarını karşılaştıralım.
%32 = 32/100 , %62 = 62/100
Kesirler konusundan da bildiğimiz gibi paydası eşit olan iki kesrin payı küçük olan küçüktür.
Dolayısıyla 32/100 < 62/100 olur.
Yani %32 < %62 dir.
Örnek : 1,28 ve 1,39 ondalık sayılarını modelleme yöntemi ile yüzdeliğe çeviriniz ve büyüklüklerini karşılaştırınız.
139 tane yüzde bir 128 tane yüzde birden daha büyüktür. Sembolle gösterirsek %139 > %128 olur.
Örnek : %34 ile %43 yüzdeliklerini yüzlük kartlarla göstererek sıralayınız.
%34 lük ve %43 lük dilimleri farklı renklerde boyarız. Sonra bu boyalı kısımları kesip üst üste koyarak büyüklüklerini karşılaştırınız.
Yüzlük kartta görüldüğü gibi üst üste konan yüzeyler arasındaki fark farklı tonlarda boyalıdır. Böylece %34’ün %43’ten küçük olduğu şekille de gösterilmiş olur.
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik Oran ve Orantı Konu Anlatımı
Oran Orantı
İki çokluğun karşılaştırılmasına oran, iki oranın eşitliğine orantı denir.
Örnek : Mert’in boyu 155 cm, kardeşininki 140 cm ise kardeşinin boyunun, Mert’in boyuna oranını bulalım.
Çözüm : Kardeşinin boyu/Mert’in boyu = 140/155 = 28/31’dir.
Örnek : 3/5 = 9/15 ifadesi bir orantı mıdır?
Çözüm :  olduğundan bu bir orantıdır.
olduğundan bu bir orantıdır.
Orantı Çeşitleri
1 kg elma 2 TL ise 5 kg elma aldığımızda kaç TL ödeneceğini miktar ve fiyata bağlı olarak tabloda gösterelim.
Miktarın fiyata oranı 1/2 ‘dir.
Orantıda terimlerin çapraz çarpımı birbirine eşittir.
1 . x = 2. 5
X = 10
Aynı sonuç kesirlerin denkliğinden yararlanarak da bulunur.
- Doğru Orantı : Bir orantıdaki iki çokluktan biri 2, 3, 4, … kat artarken diğer çokluk da 2,3,4, … kat artıyorsa ya da biri belli oranlarda azalırken diğeri de aynı oranda azalıyorsa bu orantıya doğru orantı denir. X ve y birer değişken olmak üzere aralarında y = mx bağıntısı vardır.
Örnek : 2 kg yoğurtta 120 g karbonhidrat bulunmaktadır. Aynı yoğurdun 500 g’ında kaç gram karbonhidrat vardır.
- Ters Orantı : Bir orantıdaki iki çokluktan biri 2, 3, 4, … kat artarken diğer çokluk 2, 3, 4, … kat azalıyorsa bu orantıya ters orantı denir. X ve y birer değişken olmak üzere aralarında x.y=m bağıntısı vardır.

Örnek : Bir işçi bir işi tek başına 12 günde tamamlıyor. Aynı koşullarda aynı işi 6 işçi kaç günde tamamlar?
- Bileşik Orantı
Değerleri eşit üç veya daha fazla orandan oluşan orantıya bileşik orantı denir.
Örnek : 6 işçi günde 4 saat çalışarak 100 m2 kaldırım döşemektedir. Aynı hızla çalışan 4 işçi 200 m2 kaldırım döşemesini günde kaç saat çalışarak yaparlar?
- Aynı birimler alt alta yazılır.
- Üçlü orandan biri kapatılarak diğerlerinin artıp azalmasına göre orantı çeşidi yazılır.
- Ters orantı ile bilinmeyenin üstündeki sayı; doğru orantının altındaki sayı işaretlenir.
- İşaretlenen sayılar çarpılıp diğerlerine bölünürse bilinmeyen bulunur.
Örnek : x ile y doğru orantılıdır. X = 4 iken, y = 20 ise, x = 6 iken, y kaç olur?
Çözüm : Doğru orantılı olduğundan y = mx’dir.
Yerine değerleri yazılırsa orantının sabiti bulunur. Cümlenin ikinci yarısında sabit sayı yazılarak y bulunur. Şöyle ki;
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik Denklemler Konu Anlatımı
Denklemler
Birinci Dereceden Bir Bilinmeyenli Denklemler
İçinde bilinmeyen bulunan ve bilinmeyenin aldığı değere göre doğruluğu sağlanan cebirsel ifadelere denklem denir. İçinde bir bilinmeyen bulunan ve bilinmeyenin derecesi 1 olan denklemlere birinci dereceden bir bilinmeyeli denklem denir.
Denklemin doğruluğunu sağlayan değerini bulmaya denklemi çözmek denir.
Örnek : 5x + 3 = 18 denklemini sayma pulları ile modelleyelim.
Çözümün doğruluğunu kontrol edelim.
5x + 3 = 18’de x yerine 3 yazalım.
5 . 3 + 3 = 18
15 + 3 = 18
18 = 18 olduğundan çözüm doğrudur.
5x + 3 = 18 denklemini çözümleyelim.
5x + 3 + (-3) = 18 + (-3) Bir eşitliğin her iki yanı (-3) ile toplanırsa eşitlik değişmez.
5x + 0 = 15 “0 (sıfır)” toplamada etkisiz eleman
X = 3 sonucu bulunur.
Ç = {3} veya Ç = {x = 3} olur.
Denklem çözümündeki kurallar
- Bir eşitliğin her iki yanı aynı sayı ile toplanır ya da çıkarılırsa eşitlik değişmez.
- Bir eşitliğin her iki yanı aynı sayı ile çarpılır ya da bölünürse eşitlik değişmez.
Not: Denklemler problem çözümünde kolaylık sağlar. Problem denklemle anlamlandırılarak çözümlenir.
Problem : Cem harçlığında her ay 15 TL biriktirmeye karar veriyor. Cem 300 TL’yi kaç ayda biriktirir?
Çözüm : Problemde bilinmeyene x diyerek soruyu denklemle ifade edelim.
Cem 1 ayda 15 TL biriktiriyorsa x ayda 300 TL biriktirir.
15 . x = 300 denklemiyle ifade edip çözersek;
X = 20 ay bulunur.
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik Örüntüler ve İlişkiler Konu Anlatımı
Örüntüler ve İlişkiler
- Kesme ile 2 tane parça -> 21
- Kesme ile 4 tane parça -> 22
- Kesme ile 8 tane parça -> 23
- Kesme ile 16 tane parça -> 24
. .
. .
- kesme ile 2 tane parça 2n parça oluşur.
2 sayısının n defa kendisiyle çarpılmasıyla elde edilen 2 n ifadesi bir üslü ifadedir. Burada 2 taban, n üs (kuvvet) olarak isimlendirilir.
Örneğin, 25 = 2 X 2 X 2 X 2 X
33 = 3 X 3 X 3
74 = 7 X 7 X 7 X 7
106 = 10 X 10 X 10 X 10 X 10 X 10
42 = 4 X 4
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik Cebirsel İfadeler Konu Anlatımı
Cebirsel İfadeler
Etkinlik
Kenar uzunlukları a ve b birim olan ABCD dikdörtgenin çevresini 2a + 2b, alanını ise a. b ile ifade edebiliriz.
Aynı şekilde, bir kenar uzunluğu x birim olan yandaki ABCD karesinin çevresi 4 . x , alanı x . x = x2 dir.
Yukarıda verdiğimiz örneklerde olduğu gibi anlatmak istediğimiz bir ifadeyi harfler (bilinmeyenler) yardımıyla göstermeye cebirsel ifade denir.
Örnek : 4x, 5a2, 1/3 x.y, -2x3y.z, πr2 … gibi
Not : Matematikte kullanılan bazı sabitlerle cebirsel ifadeler karıştırılmamalıdır. Harfli ifadeler, içinde bulunan değişkenin alacağı değere göre farklı değerler alır; sabitler ise değişmez.
Örneğin, π (pi) sayısı.
Terim : Bir cebirsel ifadede toplama ya da çıkarma yoluyla birbirinden ayrılan ifadelerin her birine terim denir.
Örnek : 3x2 + 4x – 8 ifadesinde 3x2, 4x, 8 ifadelerinin her biri terimdir. Bu ifadede üç terim vardır.
Not : Bir cebirsel ifadede yanında bilinmeyen bulunmayan ifadeye sabit terim denir.
4x3 – 27 ifadesinde (-27) sabit terimdir.
Sizde;
5a + 8x + 9y2 – 13y + 1/3 x3
İfadesinde kaç terim olduğunu, terimleri ayrı ayrı yazarak ve arkadaşlarınızla da tartışarak bulunuz.
Derece : Bir cebirsel ifadede herhangi bir bilinmeyenin kendisiyle kaç defa çarpılacağı gösteren ve bilinmeyenin sağ üst köşesine yazılan sabit sayıya derece denir. Derecesi en yüksek terimin derecesi, cebirsel ifadenin derecesini verir.
Örnek : 4y4 + 3x3 – 5z ifadesinde y nin derecesi 4’tür. En yüksek derece y’nin derecesi olduğundan ifade 4. derecedendir denir.
Katsayı : Cebirsel ifadelerde toplama ya da çıkarma yoluyla ayrılan terimlerin yanında çarpım olarak bulunan sabit sayılara katsayı denir.
Örnek : 16x – 25y2 . z ifadesinde x’in katsayısı 16; y2.z nin katsayısı (-25)’tir.
Not : Reel sayılar kümesi çarpma işlemine göre değişme özelliğine sahip olduğundan katsayı bilinmeyen ifadenin solunda ya da sağında olması ifadenin değerini değiştirmez, ancak işlem kolaylığı açısından katsayı genellikle soluna yazılır.
Katsayı, bir ifadenin kendisiyle kaç defa toplanacağını gösterir.
Benzer Terim : Bir cebirsel ifadede aynı dereceli terimlere benzer terim denir.
Örnek : 8x + 16X – 2/3 y2 + 5y2 cebirsel ifadesinde
8x ile 16x, -2/3 y2 ile 5y2 benzer terimlerdir.
Kategoriler: Matematik Etiketler:
7.Sınıf Matematik Rasyonel Sayılarla Adım Adım İşlemler Konu Anlatımı
Rasyonel Sayılarla Adım Adım İşlemler
Birden fazla işlem olduğu durumlarda;
Önce üslü sayılar,
Sonra parantez içindeki işlemler,
Daha sonra çarpma veya bölme işlemleri,
En son olarak da toplama veya çıkarma işlemleri yapılır.
Uyarı : Aynı önceliğe sahip işlemlerde soldan sağa doğru sıra takip edilir.
işleminin sonucunu bulalım.
Örnek :  işleminin sonucunu bulalım.
işleminin sonucunu bulalım.
Örnek : Bir sürahi 2 4/5 litre meyve suyu alıyor.
Bir barda 2/5 litre meyve suyu aldığına göre, sürahideki meyve suyunun kaç bardak geldiğini bulalım.
Çözüm : Sürahideki meyve suyunun kaç bardak geldiğini bulmak için sürahinin hacmini bir bardağın hacmine bölelim.
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik Rasyonel Sayılar Konu Anlatımı
Rasyonel Sayılar
Sayı doğrusu üzerinde; ardışık tam sayılar arasında açıkta kalan çok sayıda nokta vardır. Bu noktaların bazılarına karşılık gelen sayılar, farklı bir küme oluşturur ve aşağıdaki gibi tanımlanır.
a ve b tam sayı, b ≠ 0 olmak üzere, a/b biçiminde yazılabilen sayılara rasyonel sayılar denir. Rasyonel sayılar kümesi “Q” ile gösterilir.
Q = { …, – 3/2, -1, -3/5, 0, 1/2, 3/4, …}
Rasyonel sayılar kümesi; negatif rasyonel sayılar, pozitif rasyonel sayılar ve 0 (sıfır) dan oluşur.
Q = Q– ∪ {0} ∪ Q+
N ⊂ Z ⊂ Q dur.
Her tam sayı, paydası 1 olan rasyonel sayıdır.
Bir bütün 4 eş parçaya bölünürse;
 taralı kısım ¼ sayısı ile ifade edilir.
taralı kısım ¼ sayısı ile ifade edilir.
Örnek :
-1/3, 2/3, -7/6, ½ rasyonel sayılarını sayı doğrusunda gösterelim.
Alıştırmalar
- Aşağıda verilen sayı doğrusuna göre, A, B ve C noktalarına karşılık gelen rasyonel sayıları bulunuz.
- Sayı doğrusundaki balonların içine yazılması gereken rasyonel sayıları aşağıdakilerden seçerek yazınız.
-4/3, 4/5, 1/2, 7/2, -1/2
Rasyonel Sayılarla Toplama ve Çıkarma Konu Anlatımı
Şekilde modellenen toplama işlemine ait matematik cümlesi;
2/4 + 1/3 = 10/12’dur.
Şekilde modellenen çıkarma işlemine ait matematik cümlesi;
5/8 – 3/8 = 2/8’dir.
Sayı doğrusundaki matematik cümlesi;
6/12 + 4/12 = 10/12’dur.
Sayı doğrusundaki matematik cümlesi;
5/8 – 3/8 = 2/8’dir.
Örnek : 3 2/5 ile (-3/4) tam sayılı kesir bileşik kesre çevilir.
=(68/20) + (-15/20) paydaları eşittir.
=68-15 / 20 ortak paydaya yazılır.
= 53/20 = 2 13/20 sonuç bulunur.
Rasyonel sayılarda toplama işlemi yapılırken;
- Tam sayılı kesir, bileşik kesre çevrilir.
- Paydalar eşit değilse eşitlenir.
- Ortak paydaya yazılır.
- Paylar toplamı paya yazılarak sonuç bulunur.
- Sonuç en sade şekilde bırakılır.
Rasyonel Saylarla Çarpma ve Bölme Konu Anlatımı
Kesirlerle Çarpma İşlemi
3/5 ile 6/7 kesirlerini modelleyerek çarpalım.
Rasyonel Sayılarla Çarpma İşlemi
Örnek :  rasyonel sayılarının çarpımlarının sonucunu önce tahmin edelim.
rasyonel sayılarının çarpımlarının sonucunu önce tahmin edelim.
Sonra işlem sonucu ile tahminimizi karşılaştıralım.
Tahmin : -3
İşlem Sonucu : -2,7
Rasyonel sayılarla çarpma işlemi yaparken;
- Tam sayı ve tam sayılı kesir varsa bileşik kesre çevrilir.
- Paylar kendi aralarında, paydalar kendi aralarında çarpılacak şekilde yazılır.
- İşaretleri çarpılır.
- Varsa sadeleştirmeler yapılarak sonuç bulunur.
1. Q’da çarpma işleminin kapalılık özelliği vardır.
- Örnek :
2. Q’da çarpma işleminin değişme özelliği vardır.

3. Q’da çarpma işleminin etkisiz (birim) elemanı 1’dir. Etkisiz (birim) eleman e ile gösterilirse e = 1 ‘dir.

4. Q’da çarpma işleminin yutan elemanı 0 (sıfır) dır. Sıfırın herhangi bir sayı ile çarpımı sıfırdır.
Kategoriler: Matematik Etiketler:
7. Sınıf Matematik Tam Sayılar Konu Anlatımı
Tam Sayılar
Günlük yaşantımızda bazı kavramları ifade etmek için doğal sayılar yeterli değildir.
Sıfırdan küçük sayılara da ihtiyaç vardır.
Mesela aşağıdaki termometreleri inceleyelim.
- termometrede sıcaklık sıfırın altında 10 C (ya da – 10 C)
- termometrede sıcaklık sıfırın üstünde 20 C (ya da – 20 C) dir.
Sıfırın altındaki sıcaklıkların önüne (-), sıfırın üstündeki sıcaklıkların önüne (+) işareti konulur.
Sıfırdan büyük olan tam sayılara pozitif tam sayılar denir ve Z+ ile gösterilir.
Z+ = {+1, +2, +3, ……}
Sıfırdan küçük olan tam sayılara negatif tam sayılar denir ve Z– ile gösterilir.
Z– = {…….., -3, -2, -1}
Not : Tam sayılara aynı zamanda yönlü sayılar da denir. Bir yön pozitif (+) olduğunda, bu yönün tersi negatif (-) olur.
Örnek – 1
Bir ailenin aylık geliri 1000 TL -> +1000 TL
Bir ailenin aylık gideri 700 TL -> -700 TL
Bir malın satışından elde edilen
80 TL kar -> +80 TL
Bir malın satışından edilen
35 TL zarar -> -35 TL
Deniz seviyesinin 40 m altı -> -40m
Deniz seviyesinin 20 m üstü +20m
Not : Sıfırın işareti yoktur. Yani “0” ne negatif ne de pozitiftir.
O halde tam sayıları tanımlayacak olursak;
Negatif tam sayılar, “0” ve pozitif tam sayıların oluşturduğu kümeye tam sayılar kümesi denir ve Z ile gösterilir.
Z = Z– ∪ {0} ∪ Z+
Z 0 {…, -3, -2, -1, 0, 1, 2, 3, …}
Her tam sayıya, sayı doğrusu üzerinde bir nokta karşılık gelir ve bu noktaya o tam sayının görüntüsü denir.
Sıfır sayısının görüntüsü olan “0” noktası da başlangıç veya referans noktası denir.
Tam Sayılarda Toplama Çıkarma Konu Anlatımı
Tam Sayılarda Toplama İşlemi
- Pullarla Toplama İşlemi
Örnek : Erzurum’da hava sıcaklığı +4 C dir.
Erzurum’da hava sıcaklığı 2 C artarsa sıcaklığın kaç derece olduğunu bulalım.
Çözüm :
Erzurum’da hava sıcaklığı +6 C olur.
Örnek : Ardahan’da hava sıcaklığı -5 C dir.
Hava sıcaklığı 4 C azalırsa son durumda Ardahan’da sıcaklığın kaç derece olacağını bulalım.
Çözüm :
Ardahan’da hava sıcaklığı -9 C olur.
Örnek : (+5) + (-7) matematik cümlesini pullarla modelleyelim.
Çözüm :
Örnek : Sayma pullarıyla modellenen işlemin matematik cümlesini bulalım.
Çözüm : İşlemin matematik cümlesi, (+4) +(-3) = +1 olur.
Sayı Doğrusunda Toplama İşlemi
Sayı doğrusunda toplama işlemi yapılırken eklenen sayı pozitif ise sayı doğrusu üzerinde sağa doğru, negatif ise sola doğru gidilir.
Örnek : (+5) + (-7) matematik cümlesinin sonucunu sayı doğrusunda bulalım.
Çözüm :
(+5) + (-7) = -2 bulunur.
Toplanan tam sayılar pozitif ise bu sayıların mutlak değerleri toplanır ve elde edilen sonucun sonuna “+” işareti konur. Yani pozitif tam sayıların toplamının sonucu pozitiftir.
Örnek : (+7) + (+1) + (+12) işlemini sonucu kaçtır?
Çözüm : |+7| = 7, |+1| = 1, |+12| = 12 ise
(+7) + (+1) + (+12) = 7 + 1 + 12 = +20 dir.
Toplanan tam sayılar negatif ise bu sayıların mutlak değerleri toplanır ve elde edilen sonucun soluna “-“ işareti konur. Yani negatif tam sayıların toplamının sonucu negatiftir.
Bir Tam Sayının Toplama İşlemine Göre Tersi
Mutlak değerleri birbirine eşit zıt işaretli iki tam sayıya toplama işlemine göre birbirinin tersi denir.
O halde pozitif tam sayıların toplama işlemine göre tersi negatif, negatif tam sayıların toplama işlemine göre tersi pozitiftir. Sıfırın toplama işlemine göre tersi sıfırdır.
Tam Sayılarda Çıkarma İşlemi
- Pullarla Çıkarma İşlemi
Olduğunu öğrenmiştir.
Örnek : (-5) – (-8) işleminin sonucunu sayma pullarıyla modelleyelim.
Çözüm : -5’ten -8 çıkarabilmemiz için 3 tane daha (-) pula ihtiyacımız olduğundan 3 tane sıfır çifti ekleyelim.
8 tane (-) pulu çıkardığımızda;
3 tane (+) pulu kalır.
O halde,
(-5) – (-) = +3 olur.
Örnek : Yukarıda sayma pullarıyla modellenen işlemin matematik cümlesini bulalım.
Çözüm : 4 tane (+) pulun yanına 3 tane sıfır çifti getirilerek 7 tane (+) pul çıkarılarak geriye 3 tane (-) pul kalmıştır.
O halde işlemin matematik cümlesi;
(+4) – (+7) = -3 olur.
- Tam sayılarla Çıkarma İşlemi
A (eksilen) – B (çıkan) = C (fark)
A + (+3) = (+7) işleminde
A tam sayısı,
A = (+7) – (+3)
A = +4 olarak bulunur.
A ve b birer tam sayı olmak üzere,
(+a) – (+b) = (+a) + (-b)
(+a) – (-b) = (+a) + (+b)olur.
Örnek : (+42) – (+27) = (+42) + (-27) = +15
Örnek : (+12) – (-5) = (+12) + (+5) = +17
Örnek : (-20) – (-8) = (-20) + (+8) = -12
Örnek : (-6) – (+4) = (-6) + (-4) = -10
Tam Sayılarda Çarpma Bölme Konu Anlatımı
Tam Sayılar çarpılırken önce işaretler çarpılır, sonra sayıların mutlak değeri çarpılır.
Aynı işaretli iki sayının çarpımı (+)
Ters işaretli iki sayının çarpımı (-) dir.
Çarpma işlemi “x” işareti ile gösterildiği gibi “.” işareti ile de gösterilir.
Örnek : (+5) . (+4) = +20
Örnek : (-5) . (-4) = +20
Örnek : (+5) . (-4) = -20
Örnek : (-4) . (+5) = -20
Çarpma İşleminin Özellikleri
- Kapalılık Özelliği
İki tam sayının çarpımı yine bir tam sayıdır. Tam sayılar kümesi çarpma işlemine göre kapalıdır.
Örnek : (-2) ∈ Z ve (+3) ∈ Z iken (-2).(+3) = (-6) ∈ Z dir.
- Değişme Özelliği
İki tam sayı çarpılırken çarpanların yerleri değiştirilirse, çarpım değişmez.
Örnek : (+3).(-4) = (-4).(+3)
(-12) = (-12) değişme özelliği vardır.
- Birleşme Özelliği
Tam sayılar kümesinde çarpma işleminin birleşme özelliği vardır. Bu nedenle ikiden fazla tam sayı birbiri ile çarpılırken çarpma işlemine istediğimiz sayıdan başlayabiliriz. Çarpım değişmez.
Örnek : [(-3).(+2)](-5) = (-3).[(+2).(-5)]
(-6).(-5) = (-3).(-10)
(+30) = (+30) dur.
Birleşme özelliği vardır.
- Etkisiz Eleman
(+1) çarpma işleminin etkisiz (birim) elemanıdır. Bu nedenle bir tam sayı (+1) ile çarpıldığında, sonuç aynı tam sayıdır.
A ∈ Z iken a.(+1) = (+1).a = a dır.
Örnek : (-5).(+1) = (-5) tir.
- Yutan Eleman
Sıfırın herhangi bir sayı ile çarpımı sıfırdır. Sıfır, çarpma işlemine göre yutan elemandır.
A ∈ Z iken a.0 = 0.a = 0 dır.
Örnek : (-5).0 = 0 dır.
- Ters Eleman
İki sayının çarpımı, çarpmanın etkisiz elemanı (+1) i veriyorsa, bu iki sayı çarpma işlemine göre birbirinin tersidir.
(+1)(+1) = (+1) dir.
(-1)(-1) = (+1) dir.
(+1) ve (-1) in dışında diğer tam sayıların çarpma işlemine göre ters elemanı yoktur.
- Çarpmanın Toplama ve Çıkarma Üzerine Dağılma Özelliği
A ∈ Z, b ∈ Z, c ∈ Z ise ,
a . (b+c) = (a.b) + (a.c) dir.
- (b-c) = (a.b) – (a.c) dir.
Örnek :
(+2). [(-3) + (-4)] = [(+2).(-3)] + [(+2).(-4)]
(+2).(-7) = (-6) + (-8)
(-14) = (-14) tür.
Bölme İşlemi
Tam sayılar bölünürken, önce işaretler bölünür. Daha sonra sayıların mutlak değerleri bölünür. Aynı işaretli iki sayının bölümü pozitif, farklı işaretli iki sayının bölümü negatiftir.
Örnek : (+15) : (+3) = (+5) ya da (+15) / (+3) = (+5)
Örnek : (-24) : (-8) = (+3) ya da (-24) / (-8) = (+3)
Bölme İşleminin Özellikleri
Tam sayılar kümesinde bölme işleminin kapalılık, değişme, birleşme özellikleri ile etkisiz elemanı yoktur.
Bir tam sayının 1 e bölümü, sayının kendisine eşittir.
A : (+1) = a
Örnek : (-8) : (+1) = (-8) dir.
Sıfırın, sıfırdan farklı bir tam sayıya bölümü sıfırdır.
0/3 = 0 0:8 = 0
Sıfırdan farklı bir sayının sıfıra bölümü tanımsızdır.
A : 0 = a/0 = Tanımsız
Pozitif iki sayı arasında bölme işlemi yapılırken, parantez olmadan da bölme işlemi yapılabilr.
(+4) : ( +2) = 4 : 2 gibi.
Negatif sayılar paranteze alınarak yazılmalıdır.
(-4) : (-2) gibi
| 7. Sınıf Matematik | Açıklama | Test Linki |
| 2. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Çözümlü Sorular | Teste Başla |
| 3. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Testleri | Teste Başla |
| 4. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Test | Teste Başla |
| 5. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Testi | Teste Başla |
| 6. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Online Test | Teste Başla |
| 7. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Test Çöz | Teste Başla |
| 8. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Problemleri | Teste Başla |
| 9. Tam Sayılar | 7. Sınıf Matematik Tam Sayılar Genel Değerlendirme | Teste Başla |
| 10. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 11. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 12. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 13. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 14. Tam Sayılar | 7. Sınıf Tam Sayılar Testleri Çöz | Teste Başla |
| 15. Tam Sayılarda Toplama | 7. Sınıf Tam Sayılarda Toplama Testleri Çöz | Teste Başla |
| 16. Tam Sayılarda Çıkarma | 7. Sınıf Tam Sayılarda Çıkarma Testleri Çöz | Teste Başla |
| 17. Tam Sayılarda Çarpma | 7. Sınıf Tam Sayılarda Çarpma Testleri Çöz | Teste Başla |
| 18. Tam Sayılarda Bölme | 7. Sınıf Tam Sayılarda Bölme Testleri Çöz | Teste Başla |
| 19. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Çözümlü Sorular | Teste Başla |
| 20. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Testleri | Teste Başla |
| 21. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Test | Teste Başla |
| 22. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Testi | Teste Başla |
| 23. Tam Sayılarla Toplama Çıkarma | 7. Sınıf Tam Sayılarla Toplama Çıkarma Online Test | Teste Başla |
| 24. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Testleri | Teste Başla |
| 25. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Test | Teste Başla |
| 26. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Testi | Teste Başla |
| 27. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Online Test | Teste Başla |
| 28. Tam Sayılarla Çarpma Bölme | 7. Sınıf Tam Sayılarla Çarpma Bölme Test Çöz | Teste Başla |
Kategoriler: Matematik Etiketler: