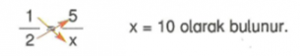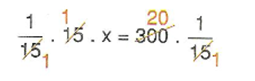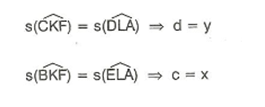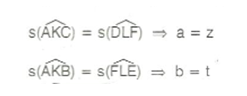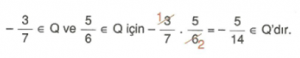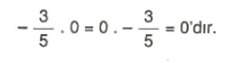7. Sınıf Fen ve Teknoloji Sindirim Sistemi Testleri Çöz
7. sınıf öğrencileri fen ve teknoloji sindirim sistemi ile ilgili testleri aşağıdaki linkleri kullanarak çözebilirsiniz. 7. sınıf fen ve teknoloji sindirim sistemi testi çöz, 7. sınıf sindirim sistemi testi çöz.
7. Sınıf Fen ve Teknoloji Boşaltım Sistemi Testleri Çöz
7. sınıf öğrencileri fen ve teknoloji boşaltım sistemi ile ilgili testleri aşağıdaki linkleri kullanarak çözebilirsiniz. 7. sınıf fen ve teknoloji boşaltım sistemi testi çöz, 7. sınıf boşaltım sistemi testi çöz.
7. Sınıf Matematik Tablo ve Grafikler Testleri Çöz
7. sınıf öğrencileri matematik tablo ve grafikler ile ilgili testleri aşağıdaki linkleri kullanarak çözebilirsiniz. 7. sınıf matematik tablo ve grafikler testi çöz, 7. sınıf tablo ve grafikler testi çöz.
7. sınıf matematik öğrencileri aşağıdaki geniş kapsamlı tablo ve grafikler testlerini çözerek okuldaki başarılarını artırabilirler. Testi bitirdiğinizde kaç doğru ve kaç yanlış yaptığınızı kontrol edebilirsiniz. Sınava başlamak için aşağıdaki “Başla” butonuna tıklayabilirsiniz.
7. sınıf tablo ve grafikler testleri her sene yeni eğitim sistemine göre güncellenmektedir. Sınavdan önce buradaki testleri çözerek okuldaki başarınızı artırabilirsiniz. En geniş kapsamlı tablo ve grafikler testlerini sitemizden çözebilirsiniz.
Toplamda 19 test ve yaklaşık 190 adet tablo ve grafikler sorusu ve konu anlatımı bulunmaktadır. Sıkılmadan çözebilesiniz diye testleri 10’ar soruluk hazırladık. Bugünkü eğitim sisteminde sınavların önemi tartışılmaz. Bu zorlu yarışta ne kadar çok test çözerseniz o kadar başarılı olursunuz. Tüm öğrencilerimize başarılar dileriz!
6. Sınıf Matematik Tablo ve Grafikler
# 6. Sınıf Matematik Tablo ve Grafikler Konu Anlatımı
# 6. Sınıf Matematik Tablo ve Grafikler 1
# 6. Sınıf Matematik Tablo ve Grafikler 2
# 6. Sınıf Matematik Tablo ve Grafikler 3
# 6. Sınıf Matematik Tablo ve Grafikler 4
# 6. Sınıf Matematik Tablo ve Grafikler 5
# 6. Sınıf Matematik Tablo ve Grafikler 6
# 6. Sınıf Matematik Tablo ve Grafikler 7
# 6. Sınıf Matematik Tablo ve Grafikler 8
# 6. Sınıf Matematik Tablo ve Grafikler 9
# 6. Sınıf Matematik Tablo ve Grafikler 10
# 6. Sınıf Matematik Tablo ve Grafikler 11
# 6. Sınıf Matematik Tablo ve Grafikler 12
# 6. Sınıf Matematik Tablo ve Grafikler 13
# 6. Sınıf Matematik Tablo ve Grafikler 14
# 6. Sınıf Matematik Tablo ve Grafikler 15
# 6. Sınıf Matematik Tablo ve Grafikler 16
# 6. Sınıf Matematik Tablo ve Grafikler 17
# 6. Sınıf Matematik Tablo ve Grafikler 18
# 6. Sınıf Matematik Tablo ve Grafikler 19
Tablo ve Grafikler Konu Anlatımı
Bir konu hakkında sonuç çıkarmak için gözlem ve araştırma yoluyla elde edilen bilgilerin sayılarla ifadesine istatistik denir.
İstatistik genel olarak geçmişi ve şimdiki durumu matematiksel tekniklerle analiz ederek, gelecek hakkında karar vermeyi sağlayan bir bilim dalıdır. Ancak biz, yapılan istatistik çalışmalarını doğru okumayı öğreneceğiz. Bu anlamda, rassal (rastgele) bir örneklemin, aritmetik ortalama, oran, mod, medyan gibi karakteristik değerlerini öğreneceğiz.
Örnek : Aşağıda, bir sınıfta öğrencilerin not dağılımını gösteren bir istatistik verilmiştir. 32 kişilik bir sınıfta, öğrencilerin Türkçe sınavından aldığı notlar ve öğrenci sayıları aşağıdaki gibidir.

Bilgi Toplama ve Bilgilerin Özetini Yapma
İstatistik çalışmalarının yapılabilmesi için belirlenen bir konuda doğru ve kesin bilgiler toplanır. Bilgileri toplama ve özetini yapmak için; anket yapma, rastgele seçme ve örnekleme olmak üzere üç yöntem kullanılır.
1. Anket Yapma :
Bu yöntemde, önceden hazırlanan sorular sorularak bilgi (veri) toplanır. Anket uygulaması bilimsel bir araştırmanın sadece veri toplama yöntemlerinden biridir. Daha sonra bu bilgiler yapılan araştırmalarda kullanılır.
Örnek : Piyasaya yeni çıkmış bir krem hakkında istatistik yapmak isteyen Gülşen aşağıdaki soruları hazırlamıştır.
I. Sürekli krem kullanır mısınız?
II. Bir kremde aradığınız özellikler nelerdir?
III. Bu kremi almaya nasıl karar verdiniz?
IV: Sonuçtan memnun musunuz?
Buna göre Gülşen hangi tip bilgi toplama ve özet yapma yöntemini kullanmıştır?
Genelleme
Rastgele Seçme
Anket Yapma
Örnekleme
Çözüm : Sadece anket yapma yönteminde önceden soru hazırlamak gerekir. Bu yüzden doğru cevap “Anket Yapma” olmalıdır.
Rastgele Seçme :
Örneğin bir televizyon kanalı yayınladığı programın izlenip izlenmediğini tespit etmek istediğinde bütün televizyon izleyicilerine ulaşamayacağı için, çeşitli kesimlerden rastgele seçtikleri kişilerin görüş ve isteklerine başvururlar. Bu şekilde yapılan araştırma yöntemine rastgele seçme denir?
Örnek : Çağlar yeni çıkan bir gazetenin Türkiye genelindeki günlük satış tirajına ait istatistikler oluşturmak için belli kesimlerden insanlar seçerek onların gazete hakkında fikirlerine başvuruyor. Buna göre, Çağlar hangi tip bilgi toplama ve özet yapma yöntemini kullanmıştır?
Genelleme
Rastgele Seçme
Anket Yapma
Örnekleme
Çözüm : Çağlar Türkiye genelindeki satışları tespit etmek için Türkiye’deki bütün insanlara ulaşamayacağı için belli bir kesim seçip orada araştırma yapıyor.
Örnekleme :
Örneğin bir çiftçinin yetiştirdiği zeytinin kalitesini belirlemek için kullanılır. Zeytinlerden örnekler alınarak bunların kalitesi incelenip, tüm zeytinlerin kalitesi tespit edilir. Bu yönteme örnekleme yöntemi denir?
Örnek : Sabun fabrikasında çalışan bir kimyager farklı maddelerle yapılmış sabunları inceliyor ve kalitelerine göre bir istatistik çıkarmayı planlıyor. Buna göre bu kimyager hangi tip bilgi toplama ve özet yapma yöntemini kullanmıştır?
Genelleme
Rastgele Seçme
Anket Yapma
Örnekleme
Çözüm : Farklı sabun örnekleri alınıp inceleniyor. İncelenmek üzere alınan her sabun bir “örnek” olduğuna göre “örnekleme” olmalıdır.
Örneklem : Üzerinde araştırma ve deney yapılacak gruba örneklem denir. Örneğin sivrisinek sayıları ile kurbağa sayıları arasında istatistik oluşturmak isteyen bir araştırmacının örneklem alanı bataklıklar olabilir. Çünkü sivrisinek ve kurbağa sayıları hakkındaki verilere en rahat bataklıkta ulaşılabilir.
Örnek : Özlem fast food yiyeceklerle beslenen insandaki kilo artışı üzerine bir istatistik yapmak istiyor. Bu konu hakkında anket yaparak veri toplamak isteyen Özlem’in örneklem alanı neresi olabilir?
Okullardaki 10. Sınıf öğrencileri
Oturduğu apartmandaki insanlar
Babasının iş arkadaşları
Fast food yiyeceklerin satıldığı bir yerdeki müşteriler
Çözüm : Fast food yiyeceklerle beslenen insanlara ulaşmak için en iyi yol, fast food yiyeceklerinin satıldığı yerlerdir.
Tablo Oluşturma :
Toplanan veriler, uygun bir tablo oluşturarak çetele şeklinde yazılır. Yapılan tabloya muhakkak bir başlık yazılmalıdır. Bu tabloları yorum yapmak için de kullanacağız. Daha sonra oluşturduğumuz bu tabloları grafik haline dönüştürmeyi öğreneceğiz.
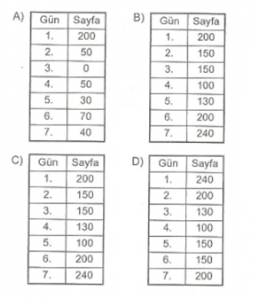
Örnek : Ebru pazartesi 200, Salı 150, Çarşamba 150, Perşembe 100, Pazar 240 sayfa kitap okuyor. Ebru’nun kitap okuma istatistiğini çıkarmak için bir tablo hazırlayan öğretmeni aşağıdaki tablolardan hangisini yapmalıdır?
Çözüm : Haftanın günleri 1, 2, 3, …….. şeklinde göstermek üzere okunan sayfa sayılarını tabloya yerleştirmeliyiz. Doğru yanıt “B” seçeneğidir.
Grafik Çeşitleri :
Verileri toplayıp özetledikten sonra bunları resim, şekil veya çizgiler yardımıyla gösteririz. Bu gösterime grafik denir. Grafikler istatistiki bilgileri anlamayı kolaylaştırır.
1. Çizgi Grafiği
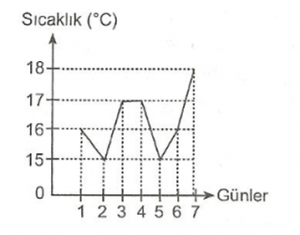
Yukarıdaki grafik, bir ilin Mayıs ayının ilk haftasına ait, sıcaklık değerlerini göstermektedir. Örneğin 5. gün sıcaklık 15 derece olur.
2. Sütun Grafiği
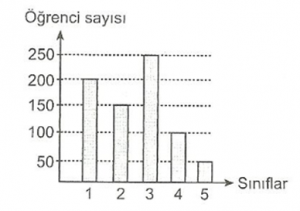
Yukarıdaki grafikte bir okulun sınıflarındaki öğrenci sayıları gösterilmiştir.
Grafiğe göre;
1. sınıfta 200 öğrenci, 2. Sınıfta 150 öğrenci, 3. Sınıfta 250 öğrenci, 4. Sınıfta 100 öğrenci ve 5. Sınıfta 50 öğrenci görmektedir.
3. Şekil Grafiği
Bir sınıftaki öğrencileri şekil grafiğiyle gösterelim.
Grafiğe göre;
Erkek öğrenci sayısı: 4 X 5 = 20 kişi
Kız öğrenci sayısı : 3 X 5 = 15
Sınıfta toplam : 20 + 15 = 35 öğrenci vardır.
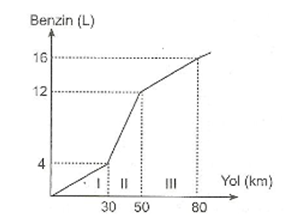
Örnek :
Yukarıdaki şekil bir arabanın aldığı yola göre harcadığı benzin miktarını göstermektedir. Buna göre aşağıdakilerden hangisi yanlıştır?
a) İlk 50 km’de harcanan benzin miktarı ile son 50 km’de harcanan benzin miktarı aynıdır.
b) İlk 30 km’de harcanan benzin miktarı ile son 30 km’de harcanan benzin miktarı birbirine eşittir.
c) En çok benzin III aralığında kullanılmıştır.
d) En çok benzin II aralığında kullanılmıştır.
Çözüm : Seçenekleri sırayla inceleyelim:
a) İlk 50 km’de 12 L, son 50 km’de 16 – 4 = 12 L benzin kullanılmıştır.
b) İlk 30 km’de 4 L, son 30 km’de 16 – 12 = 4L benzin kullanılmıştır.
c) I aralığında 4 L, II aralığında 12 – 4 = 8 L, III aralığında 16 – 12 = 4 L benzin kullanılmıştır. En çok benzin II aralığında kullanılmıştır.
d) En çok benzin II aralığında kullanılmıştır.
Doğru yanıt “C” seçeneğidir.
7. Sınıf Matematik Oran ve Orantı Testleri Çöz
7. sınıf matematik öğrencileri aşağıdaki geniş kapsamlı oran orantı testlerini çözerek okuldaki başarılarını artırabilirler. Testi bitirdiğinizde kaç doğru ve kaç yanlış yaptığınızı kontrol edebilirsiniz. Sınava başlamak için aşağıdaki “Başla” butonuna tıklayabilirsiniz.
7. sınıf oran orantı testleri her sene yeni eğitim sistemine göre güncellenmektedir. Sınavdan önce buradaki testleri çözerek okuldaki başarınızı artırabilirsiniz. En geniş kapsamlı oran orantı testlerini sitemizden çözebilirsiniz.
Toplamda 1 tanesi çözümlü 16 test ve yaklaşık 160 adet oran orantı sorusu ve konu anlatımı bulunmaktadır. Sıkılmadan çözebilesiniz diye testleri 10’ar soruluk hazırladık. Bugünkü eğitim sisteminde sınavların önemi tartışılmaz. Bu zorlu yarışta ne kadar çok test çözerseniz o kadar başarılı olursunuz. Tüm öğrencilerimize başarılar dileriz!
7. sınıf öğrencileri matematik oran ve orantı ile ilgili testleri aşağıdaki linkleri kullanarak çözebilirsiniz. 7. sınıf matematik oran ve orantı testi çöz, 7. sınıf oran ve orantı testi çöz.
| 7. Sınıf Oran Orantı | Açıklama | Test Linki |
| Oran Orantı | 7. Sınıf Matematik Oran Orantı Konu Anlatımı | Konu Anlatımı |
| Oran Orantı (1) | 7. Sınıf Matematik Oran Orantı Çözümlü Sorular | Teste Başla |
| Oran Orantı (2) | 7. Sınıf Matematik Oran Orantı Testleri | Teste Başla |
| Oran Orantı (3) | 7. Sınıf Matematik Oran Orantı Test | Teste Başla |
| Oran Orantı (4) | 7. Sınıf Matematik Oran Orantı Testi | Teste Başla |
| Oran Orantı (5) | 7. Sınıf Matematik Oran Orantı Online Test | Teste Başla |
| Oran Orantı (6) | 7. Sınıf Matematik Oran Orantı Test Çöz | Teste Başla |
| Oran Orantı (7) | 7. Sınıf Matematik Oran Orantı Problemleri | Teste Başla |
| Oran Orantı (8) | 7. Sınıf Matematik Oran Orantı Soruları | Teste Başla |
| Oran Orantı (9) | 7. Sınıf Matematik Oran Orantı İle İlgili Sorular | Teste Başla |
| Oran Orantı (10) | 7. Sınıf Matematik Oran Orantı İle İlgili Test Çöz | Teste Başla |
| Oran Orantı (11) | 7. Sınıf Matematik Oran Orantı Genel Değerlendirme | Teste Başla |
| Oran Orantı (12) | 7. Sınıf Matematik Oran Orantı Deneme Sınavı | Teste Başla |
| Oran ve Orantı (13) | 7. Sınıf Oran ve Orantı Testleri | Testi Çöz |
| Oran ve Orantı (14) | 7. Sınıf Oran ve Orantı Testleri | Testi Çöz |
| Oran ve Orantı (15) | 7. Sınıf Oran ve Orantı Testleri | Testi Çöz |
| Oran ve Orantı (16) | 7. Sınıf Oran ve Orantı Testleri | Testi Çöz |
Oran Orantı Konu Anlatımı
İki çokluğun karşılaştırılmasına oran, iki oranın eşitliğine orantı denir.
Örnek : Mert’in boyu 155 cm, kardeşininki 140 cm ise kardeşinin boyunun, Mert’in boyuna oranını bulalım.
Çözüm : Kardeşinin boyu/Mert’in boyu = 140/155 = 28/31’dir.
Örnek : 3/5 = 9/15 ifadesi bir orantı mıdır?
Çözüm :  olduğundan bu bir orantıdır.
olduğundan bu bir orantıdır.
Orantı Çeşitleri
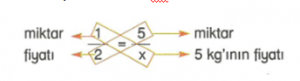
1 kg elma 2 TL ise 5 kg elma aldığımızda kaç TL ödeneceğini miktar ve fiyata bağlı olarak tabloda gösterelim.
Miktarın fiyata oranı 1/2 ‘dir.
Orantıda terimlerin çapraz çarpımı birbirine eşittir.
1 . x = 2. 5
X = 10
Aynı sonuç kesirlerin denkliğinden yararlanarak da bulunur.
- Doğru Orantı : Bir orantıdaki iki çokluktan biri 2, 3, 4, … kat artarken diğer çokluk da 2,3,4, … kat artıyorsa ya da biri belli oranlarda azalırken diğeri de aynı oranda azalıyorsa bu orantıya doğru orantı denir. X ve y birer değişken olmak üzere aralarında y = mx bağıntısı vardır.
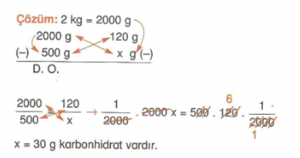
Örnek : 2 kg yoğurtta 120 g karbonhidrat bulunmaktadır. Aynı yoğurdun 500 g’ında kaç gram karbonhidrat vardır.
- Ters Orantı : Bir orantıdaki iki çokluktan biri 2, 3, 4, … kat artarken diğer çokluk 2, 3, 4, … kat azalıyorsa bu orantıya ters orantı denir. X ve y birer değişken olmak üzere aralarında x.y=m bağıntısı vardır.

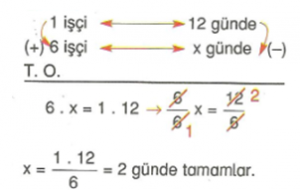
Örnek : Bir işçi bir işi tek başına 12 günde tamamlıyor. Aynı koşullarda aynı işi 6 işçi kaç günde tamamlar?
- Bileşik Orantı
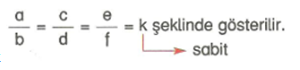
Değerleri eşit üç veya daha fazla orandan oluşan orantıya bileşik orantı denir.
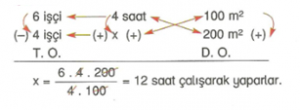
Örnek : 6 işçi günde 4 saat çalışarak 100 m2 kaldırım döşemektedir. Aynı hızla çalışan 4 işçi 200 m2 kaldırım döşemesini günde kaç saat çalışarak yaparlar?
- Aynı birimler alt alta yazılır.
- Üçlü orandan biri kapatılarak diğerlerinin artıp azalmasına göre orantı çeşidi yazılır.
- Ters orantı ile bilinmeyenin üstündeki sayı; doğru orantının altındaki sayı işaretlenir.
- İşaretlenen sayılar çarpılıp diğerlerine bölünürse bilinmeyen bulunur.
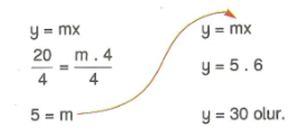
Örnek : x ile y doğru orantılıdır. X = 4 iken, y = 20 ise, x = 6 iken, y kaç olur?
Çözüm : Doğru orantılı olduğundan y = mx’dir.
Yerine değerleri yazılırsa orantının sabiti bulunur. Cümlenin ikinci yarısında sabit sayı yazılarak y bulunur. Şöyle ki;
Kategoriler: Matematik Etiketler: 7. sınıf oran ve orantı testi, 7. sınıf oran ve orantı testi çöz, 7. sınıf oran ve orantı testleri
7. Sınıf Matematik Denklemler Testleri Çöz
7. sınıf matematik öğrencileri aşağıdaki geniş kapsamlı denklemler testlerini çözerek okuldaki başarılarını artırabilirler. Testi bitirdiğinizde kaç doğru ve kaç yanlış yaptığınızı kontrol edebilirsiniz. Sınava başlamak için aşağıdaki “Başla” butonuna tıklayabilirsiniz.
7. sınıf denklemler testleri her sene yeni eğitim sistemine göre güncellenmektedir. Sınavdan önce buradaki testleri çözerek okuldaki başarınızı artırabilirsiniz. En geniş kapsamlı denklemler testlerini sitemizden çözebilirsiniz.
Toplamda 1 tanesi çözümlü 20 test ve yaklaşık 200 adet denklemler sorusu ve konu anlatımı bulunmaktadır. Sıkılmadan çözebilesiniz diye testleri 10’ar soruluk hazırladık. Bugünkü eğitim sisteminde sınavların önemi tartışılmaz. Bu zorlu yarışta ne kadar çok test çözerseniz o kadar başarılı olursunuz. Tüm öğrencilerimize başarılar dileriz!
7. sınıf öğrencileri matematik denklemler ile ilgili testleri aşağıdaki linkleri kullanarak çözebilirsiniz. 7. sınıf matematik denklemler testi çöz, 7. sınıf denklemler testi çöz.
| 7. Sınıf Matematik | Açıklama | Test Linki |
| Denklemler | 7. Sınıf Matematik Denklemler Konu Anlatımı | Konu Anlatımı |
| Denklemler (1) | 7. Sınıf Matematik Denklemler Çözümlü Sorular | Teste Başla |
| Denklemler (2) | 7. Sınıf Matematik Denklemler Testleri | Teste Başla |
| Denklemler (3) | 7. Sınıf Matematik Denklemler Test | Teste Başla |
| Denklemler (4) | 7. Sınıf Matematik Denklemler Testi | Teste Başla |
| Denklemler (5) | 7. Sınıf Matematik Denklemler Online Test | Teste Başla |
| Denklemler (6) | 7. Sınıf Matematik Denklemler Test Çöz | Teste Başla |
| Denklemler (7) | 7. Sınıf Matematik Denklemler Problemleri | Teste Başla |
| Denklemler (8) | 7. Sınıf Matematik Denklemler Soruları | Teste Başla |
| Denklemler (9) | 7. Sınıf Matematik Denklemler İle İlgili Sorular | Teste Başla |
| Denklemler (10) | 7. Sınıf Matematik Denklemler İle İlgili Test Çöz | Teste Başla |
| Denklemler (11) | 7. Sınıf Matematik Denklemler Testi Çöz | Teste Başla |
| Denklemler (12) | 7. Sınıf Matematik Denklemler Soru Çöz | Teste Başla |
| Denklemler (13) | 7. Sınıf Matematik Denklemler Genel Değerlendirme | Teste Başla |
| Denklemler (14) | 7. Sınıf Matematik Denklemler Konu Tarama | Teste Başla |
| Denklemler (15) | 7. Sınıf Matematik Denklemler Deneme Sınavı | Teste Başla |
| Denklemler (16) | 7. Sınıf Matematik Denklemler TEOG Hazırlık | Teste Başla |
| Denklemler (17) | 7. Sınıf Denklemler Testleri | Testi Çöz |
| Denklemler (18) | 7. Sınıf Denklemler Testleri | Testi Çöz |
| Denklemler (19) | 7. Sınıf Denklemler Testleri | Testi Çöz |
| Denklemler (20) | 7. Sınıf Denklemler Testleri | Testi Çöz |
Birinci Dereceden Bir Bilinmeyenli Denklemler
İçinde bilinmeyen bulunan ve bilinmeyenin aldığı değere göre doğruluğu sağlanan cebirsel ifadelere denklem denir. İçinde bir bilinmeyen bulunan ve bilinmeyenin derecesi 1 olan denklemlere birinci dereceden bir bilinmeyeli denklem denir.
Denklemin doğruluğunu sağlayan değerini bulmaya denklemi çözmek denir.
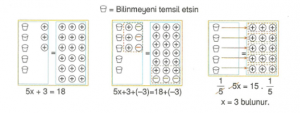
Örnek : 5x + 3 = 18 denklemini sayma pulları ile modelleyelim.
Çözümün doğruluğunu kontrol edelim.
5x + 3 = 18’de x yerine 3 yazalım.
5 . 3 + 3 = 18
15 + 3 = 18
18 = 18 olduğundan çözüm doğrudur.
5x + 3 = 18 denklemini çözümleyelim.
5x + 3 + (-3) = 18 + (-3) Bir eşitliğin her iki yanı (-3) ile toplanırsa eşitlik değişmez.
5x + 0 = 15 “0 (sıfır)” toplamada etkisiz eleman
X = 3 sonucu bulunur.
Ç = {3} veya Ç = {x = 3} olur.
Denklem çözümündeki kurallar
- Bir eşitliğin her iki yanı aynı sayı ile toplanır ya da çıkarılırsa eşitlik değişmez.
- Bir eşitliğin her iki yanı aynı sayı ile çarpılır ya da bölünürse eşitlik değişmez.
Not: Denklemler problem çözümünde kolaylık sağlar. Problem denklemle anlamlandırılarak çözümlenir.
Problem : Cem harçlığında her ay 15 TL biriktirmeye karar veriyor. Cem 300 TL’yi kaç ayda biriktirir?
Çözüm : Problemde bilinmeyene x diyerek soruyu denklemle ifade edelim.
Cem 1 ayda 15 TL biriktiriyorsa x ayda 300 TL biriktirir.
15 . x = 300 denklemiyle ifade edip çözersek;
X = 20 ay bulunur.
Kategoriler: Matematik Etiketler: 7. sınıf denklemler testi, 7. sınıf denklemler testleri, 7. sınıf denklemler testleri çöz
7. Sınıf Matematik Doğrular ve Açılar Testleri Çöz
7. sınıf matematik öğrencileri aşağıdaki geniş kapsamlı doğrular ve açılar testlerini çözerek okuldaki başarılarını artırabilirler. Testi bitirdiğinizde kaç doğru ve kaç yanlış yaptığınızı kontrol edebilirsiniz. Sınava başlamak için aşağıdaki “Başla” butonuna tıklayabilirsiniz.
7. sınıf doğrular ve açılar testleri her sene yeni eğitim sistemine göre güncellenmektedir. Sınavdan önce buradaki testleri çözerek okuldaki başarınızı artırabilirsiniz. En geniş kapsamlı doğrular ve açılar testlerini sitemizden çözebilirsiniz.
Toplamda 1 tanesi çözümlü 11 test ve yaklaşık 110 adet doğrular ve açılar sorusu ve konu anlatımı bulunmaktadır. Sıkılmadan çözebilesiniz diye testleri 10’ar soruluk hazırladık. Bugünkü eğitim sisteminde sınavların önemi tartışılmaz. Bu zorlu yarışta ne kadar çok test çözerseniz o kadar başarılı olursunuz. Tüm öğrencilerimize başarılar dileriz!
7. sınıf öğrencileri matematik doğrular ve açılar ile ilgili testleri aşağıdaki linkleri kullanarak çözebilirsiniz. 7. sınıf matematik doğrular ve açılar testi çöz, 7. sınıf doğrular ve açılar testi çöz.
| 7. Sınıf Doğrular ve Açılar | Açıklama | Test Linki |
| Doğrular ve Açılar | 7. Sınıf Matematik Doğrular ve Açılar Konu Anlatımı | Konu Anlatımı |
| Doğrular ve Açılar | 7. Sınıf Matematik Doğrular ve Açılar Çözümlü Sorular | Teste Başla |
| Doğrular ve Açılar (1) | 7. Sınıf Matematik Doğrular ve Açılar Testleri | Teste Başla |
| Doğrular ve Açılar (2) | 7. Sınıf Matematik Doğrular ve Açılar Test | Teste Başla |
| Doğrular ve Açılar (3) | 7. Sınıf Matematik Doğrular ve Açılar Testi | Teste Başla |
| Doğrular ve Açılar (4) | 7. Sınıf Matematik Doğrular ve Açılar Online Test | Teste Başla |
| Doğrular ve Açılar (5) | 7. Sınıf Matematik Doğrular ve Açılar Test Çöz | Teste Başla |
| Doğrular ve Açılar (6) | 7. Sınıf Matematik Doğrular ve Açılar Soruları | Teste Başla |
| Doğrular ve Açılar (7) | 7. Sınıf Matematik Doğrular ve Açılar Genel Değerlendirme | Teste Başla |
| Doğrular ve Açılar (8) | 7. Sınıf Doğrular ve Açılar Deneme Sınavı 1 | Testi Çöz |
| Doğrular ve Açılar (9) | 7. Sınıf Doğrular ve Açılar Deneme Sınavı 2 | Testi Çöz |
| Doğrular ve Açılar (10) | 7. Sınıf Doğrular ve Açılar Deneme Sınavı 3 | Testi Çöz |
Doğrular ve Açılar Konu Anlatımı
A. Düzlemde Doğrular
1. Bir noktanın bir doğruya olan en kısa uzaklığı
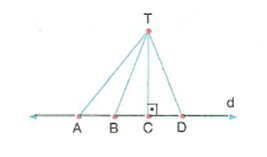
Bir noktanın bir doğruya olan en kısa uzaklığı, bu noktadan doğruya çizilen dikmenin uzunluğudur.
Yukarıdaki şekilde [TC] ⊥ d olduğundan T noktasının d doğrusuna en kısa uzaklığı |TC| dir.
2. Bir doğru parçasının orta dikmesi
Bir doğru parçasının orta dikmesi, bu doğru parçasını iki eş parçaya ayırır. Ayrıca orta dikme üzerindeki noktaların doğru parçasının uç noktalarına olan uzaklıkları birbirine eşittir.
Yukarıdaki şekilde [KC] ⊥ [AB] ve |AC| = |CB| olduğundan |TA| = |TB| ve |KA| =|KB| dir.
3. Bir Düzlemde İki Doğrunun Birbirine Göre Durumları
Çakışık Doğrular :
Aynı düzlemde ve aynı iki noktadan geçen doğrulara çakışık doğrular denir.
Kesişen Doğrular :
Aynı düzlemde yalnız bir ortak noktası bulunan doğrulara kesişen doğrular denir.
Dik Doğrular :
Aynı düzlem üzerinde bulup, birbirini dik olarak kesen doğrulardır.
Paralel Doğrular :
Aynı düzlem üzerinde bulunan ve birbirlerini hiç kesmeyen, ortak noktası bulunmayan doğrulardır.
4. Bir Düzlemde Farklı Üç Doğrunun Birbirine Göre Durumları
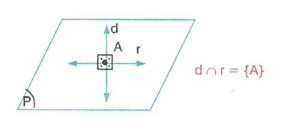
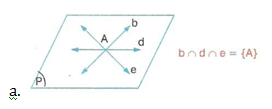
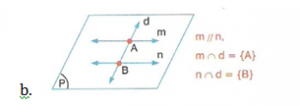
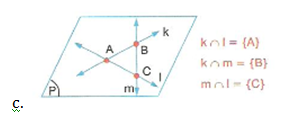
Bir düzlemde bulunan üç farklı doğru birbirine göre dört farklı durumda bulunurlar.
Bu durumlar,
b, d ve e doğruları bir A noktasında kesişirler.
m ile n paralel, d doğrusu ise bu iki doğruyu, farklı iki noktadan kesmektedir.
üç doğru birbirini üç farklı noktada keserler.
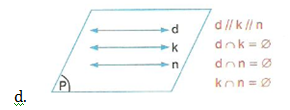
d, k ve n doğruları paraleldir.
B. Paralel İki Doğrunun Bir Kesenle Yaptığı Açılar
Paralel iki doğruyu üçüncü bir doğrunun kesmesiyle oluşan açılardır.
1. Yöndeş Açılar :
Paralel iki doğruyu üçüncü bir doğrunun kesmesiyle oluşan açılardan aynı yöne bakan açılara yöndeş açılar denir.
Şekilde ;
Yöndeş açıların ölçüleri birbirine eşittir.
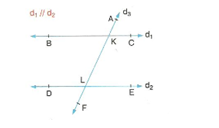
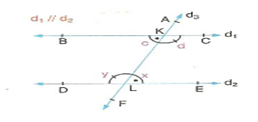
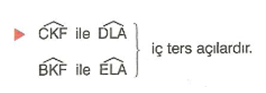
2. İç Ters Açılar
Şekildeki
İç ters açılarının ölçüleri birbirine eşittir.
3. Dış Ters Açılar
Şekilde;
Dış ters açılarının ölçüleri birbirine eşittir.
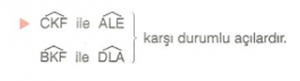
4. Karşı Durumlu Açılar
Şekilde;
Karşı durumlu açılar bütünler açılardır.
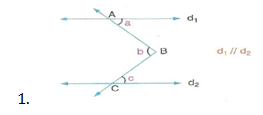
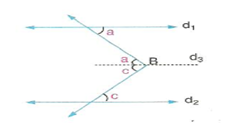
Özel Durumlar
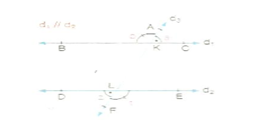
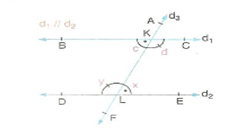
Şekilde; b = a+c’dir.
Şekilde görüldüğü gibi B köşesinden d ve d doğrularına paralel d doğrusu çizersek iç ters açılar oluşur. b = a + c olduğu görülür.
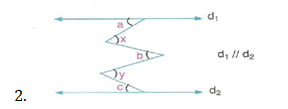
Paralel çizgiler arasında zikzak çizildiğinde, bir tarafa bakan açıların ölçüleri toplamı diğer tarafa bakan açıların ölçüleri toplamına eşittir.
a + b + c = x + y
[AB // [DE ise;
a + b + c = 360° dir.
[AB ve [DE ye paralel [CF çizilirse iç ters açılardan a + b + c = 360° bulunur.
7. Sınıf Matematik Rasyonel Sayılar Testleri Çöz
7. sınıf matematik öğrencileri aşağıdaki geniş kapsamlı rasyonel sayılar testlerini çözerek okuldaki başarılarını artırabilirler. Testi bitirdiğinizde kaç doğru ve kaç yanlış yaptığınızı kontrol edebilirsiniz. Sınava başlamak için aşağıdaki “Başla” butonuna tıklayabilirsiniz.
7. sınıf rasyonel sayılar testleri her sene yeni eğitim sistemine göre güncellenmektedir. Sınavdan önce buradaki testleri çözerek okuldaki başarınızı artırabilirsiniz. En geniş kapsamlı rasyonel sayılar testlerini sitemizden çözebilirsiniz.
Toplamda 32 test ve yaklaşık 320 adet rasyonel sayılar sorusu ve konu anlatımı bulunmaktadır. Sıkılmadan çözebilesiniz diye testleri 10’ar soruluk hazırladık. Bugünkü eğitim sisteminde sınavların önemi tartışılmaz. Bu zorlu yarışta ne kadar çok test çözerseniz o kadar başarılı olursunuz. Tüm öğrencilerimize başarılar dileriz!
7. sınıf öğrencileri matematik rasyonel sayılar ile ilgili testleri aşağıdaki linkleri kullanarak çözebilirsiniz. 7. sınıf matematik rasyonel sayılar testi çöz, 7. sınıf rasyonel sayılarda sıralama testi çöz.
| 7. Sınıf Matematik | Açıklama | Test Linki |
| Rasyonel Sayılar | 7. Sınıf Matematik Rasyonel Sayılar Konu Anlatımı | Konu Anlatımı |
| Rasyonel Sayılar (1) | 7. Sınıf Matematik Rasyonel Sayılar Çözümlü Sorular | Teste Başla |
| Rasyonel Sayılar (2) | 7. Sınıf Matematik Rasyonel Sayılar Testleri | Teste Başla |
| Rasyonel Sayılar (3) | 7. Sınıf Matematik Rasyonel Sayılar Test | Teste Başla |
| Rasyonel Sayılar (4) | 7. Sınıf Matematik Rasyonel Sayılar Testi | Teste Başla |
| Rasyonel Sayılar (5) | 7. Sınıf Matematik Rasyonel Sayılar Online Test | Teste Başla |
| Rasyonel Sayılar (6) | 7. Sınıf Matematik Rasyonel Sayılar Test Çöz | Teste Başla |
| Rasyonel Sayılar (7) | 7. Sınıf Matematik Rasyonel Sayılar Problemleri | Teste Başla |
| Rasyonel Sayılar (8) | 7. Sınıf Matematik Rasyonel Sayılar Soruları | Teste Başla |
| Rasyonel Sayılar (9) | 7. Sınıf Matematik Rasyonel Sayılar İle İlgili Sorular | Teste Başla |
| Rasyonel Sayılar (10) | 7. Sınıf Matematik Rasyonel Sayılar İle İlgili Test Çöz | Teste Başla |
| Rasyonel Sayılar (11) | 7. Sınıf Matematik Rasyonel Sayılar Testi Çöz | Teste Başla |
| Rasyonel Sayılar (12) | 7. Sınıf Matematik Rasyonel Sayılar Genel Değerlendirme | Teste Başla |
| Rasyonel Sayılar (13) | 7. Sınıf Matematik Rasyonel Sayılar Konu Tarama | Teste Başla |
| Rasyonel Sayılarla Toplama Çıkarma (14) | 7. Sınıf Matematik Rasyonel Sayılarla Toplama Çıkarma Testleri | Teste Başla |
| Rasyonel Sayılarla Toplama Çıkarma (15) | 7. Sınıf Matematik Rasyonel Sayılarla Toplama Çıkarma Test | Teste Başla |
| Rasyonel Sayılarla Toplama Çıkarma (16) | 7. Sınıf Matematik Rasyonel Sayılarla Toplama Çıkarma Testi | Teste Başla |
| Rasyonel Sayılarla Toplama Çıkarma (17) | 7. Sınıf Matematik Rasyonel Sayılarla Toplama Çıkarma Online Test | Teste Başla |
| Rasyonel Sayılarla Toplama Çıkarma (18) | 7. Sınıf Matematik Rasyonel Sayılarla Toplama Çıkarma Test Çöz | Teste Başla |
| Rasyonel Sayılarla Toplama Çıkarma (19) | 7. Sınıf Matematik Rasyonel Sayılarla Toplama Çıkarma Problemleri | Teste Başla |
| Rasyonel Sayılarla Toplama Çıkarma (20) | 7. Sınıf Matematik Rasyonel Sayılarla Toplama Çıkarma Soruları | Teste Başla |
| Rasyonel Sayılarla Toplama Çıkarma (21) | 7. Sınıf Matematik Rasyonel Sayılarla Toplama Çıkarma İle İlgili Sorular | Teste Başla |
| Rasyonel Sayılarla Toplama Çıkarma (22) | 7. Sınıf Matematik Rasyonel Sayılarla Toplama Çıkarma İle İlgili Test Çöz | Teste Başla |
| Rasyonel Sayılarla Toplama Çıkarma (23) | 7. Sınıf Matematik Rasyonel Sayılarla Toplama Çıkarma Genel Değerlendirme | Teste Başla |
| Rasyonel Sayılarla Çarpma Bölme (24) | 7. Sınıf Matematik Rasyonel Sayılarla Çarpma Bölme Testleri | Teste Başla |
| Rasyonel Sayılarla Çarpma Bölme (25) | 7. Sınıf Matematik Rasyonel Sayılarla Çarpma Bölme Test | Teste Başla |
| Rasyonel Sayılarla Çarpma Bölme (26) | 7. Sınıf Matematik Rasyonel Sayılarla Çarpma Bölme Testi | Teste Başla |
| Rasyonel Sayılarla Çarpma Bölme (27) | 7. Sınıf Matematik Rasyonel Sayılarla Çarpma Bölme Online Test | Teste Başla |
| Rasyonel Sayılarla Çarpma Bölme (28) | 7. Sınıf Matematik Rasyonel Sayılarla Çarpma Bölme Test Çöz | Teste Başla |
| Rasyonel Sayılarla Çarpma Bölme (29) | 7. Sınıf Matematik Rasyonel Sayılarla Çarpma Bölme Problemleri | Teste Başla |
| Rasyonel Sayılarla Çarpma Bölme (30) | 7. Sınıf Matematik Rasyonel Sayılarla Çarpma Bölme Soruları | Teste Başla |
| Rasyonel Sayılarla Çarpma Bölme (31) | 7. Sınıf Matematik Rasyonel Sayılarla Çarpma Bölme Genel Değerlendirme | Teste Başla |
| Rasyonel Sayılar (32) | 7. Sınıf Rasyonel Sayılar Testleri | Testi Çöz |
Rasyonel Sayılar Konu Anlatımı
Sayı doğrusu üzerinde; ardışık tam sayılar arasında açıkta kalan çok sayıda nokta vardır. Bu noktaların bazılarına karşılık gelen sayılar, farklı bir küme oluşturur ve aşağıdaki gibi tanımlanır.
a ve b tam sayı, b ≠ 0 olmak üzere, a/b biçiminde yazılabilen sayılara rasyonel sayılar denir. Rasyonel sayılar kümesi “Q” ile gösterilir.
Q = { …, – 3/2, -1, -3/5, 0, 1/2, 3/4, …}
Rasyonel sayılar kümesi; negatif rasyonel sayılar, pozitif rasyonel sayılar ve 0 (sıfır) dan oluşur.
Q = Q– ∪ {0} ∪ Q+
N ⊂ Z ⊂ Q dur.
Her tam sayı, paydası 1 olan rasyonel sayıdır.
Bir bütün 4 eş parçaya bölünürse;
 taralı kısım ¼ sayısı ile ifade edilir.
taralı kısım ¼ sayısı ile ifade edilir.
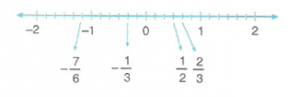
Örnek :
-1/3, 2/3, -7/6, ½ rasyonel sayılarını sayı doğrusunda gösterelim.
Alıştırmalar
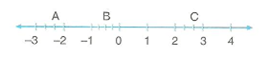
- Aşağıda verilen sayı doğrusuna göre, A, B ve C noktalarına karşılık gelen rasyonel sayıları bulunuz.
- Sayı doğrusundaki balonların içine yazılması gereken rasyonel sayıları aşağıdakilerden seçerek yazınız.
-4/3, 4/5, 1/2, 7/2, -1/2
Rasyonel Sayılarla Toplama ve Çıkarma Konu Anlatımı
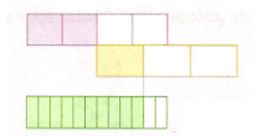
Şekilde modellenen toplama işlemine ait matematik cümlesi;
2/4 + 1/3 = 10/12’dur.
Şekilde modellenen çıkarma işlemine ait matematik cümlesi;
5/8 – 3/8 = 2/8’dir.
Sayı doğrusundaki matematik cümlesi;
6/12 + 4/12 = 10/12’dur.
Sayı doğrusundaki matematik cümlesi;
5/8 – 3/8 = 2/8’dir.
Örnek : 3 2/5 ile (-3/4) tam sayılı kesir bileşik kesre çevilir.
=(68/20) + (-15/20) paydaları eşittir.
=68-15 / 20 ortak paydaya yazılır.
= 53/20 = 2 13/20 sonuç bulunur.
Rasyonel sayılarda toplama işlemi yapılırken;
- Tam sayılı kesir, bileşik kesre çevrilir.
- Paydalar eşit değilse eşitlenir.
- Ortak paydaya yazılır.
- Paylar toplamı paya yazılarak sonuç bulunur.
- Sonuç en sade şekilde bırakılır.
Rasyonel Saylarla Çarpma ve Bölme Konu Anlatımı
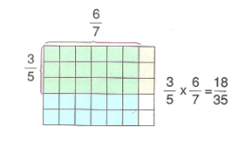
Kesirlerle Çarpma İşlemi
3/5 ile 6/7 kesirlerini modelleyerek çarpalım.
Rasyonel Sayılarla Çarpma İşlemi
Örnek :  rasyonel sayılarının çarpımlarının sonucunu önce tahmin edelim.
rasyonel sayılarının çarpımlarının sonucunu önce tahmin edelim.
Sonra işlem sonucu ile tahminimizi karşılaştıralım.
Tahmin : -3
İşlem Sonucu : -2,7
Rasyonel sayılarla çarpma işlemi yaparken;
- Tam sayı ve tam sayılı kesir varsa bileşik kesre çevrilir.
- Paylar kendi aralarında, paydalar kendi aralarında çarpılacak şekilde yazılır.
- İşaretleri çarpılır.
- Varsa sadeleştirmeler yapılarak sonuç bulunur.
1. Q’da çarpma işleminin kapalılık özelliği vardır.
-
- Örnek :
2. Q’da çarpma işleminin değişme özelliği vardır.
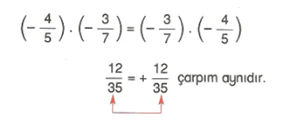
3. Q’da çarpma işleminin etkisiz (birim) elemanı 1’dir. Etkisiz (birim) eleman e ile gösterilirse e = 1 ‘dir.

4. Q’da çarpma işleminin yutan elemanı 0 (sıfır) dır. Sıfırın herhangi bir sayı ile çarpımı sıfırdır.
7. Sınıf Din Kültürü ve Ahlak Bilgisi Testleri
| 7. Sınıf Din Kültürü | Açıklama | Online Test Linkleri |
|---|---|---|
| Test 1 | 7. Sınıf Din Kültürü Testleri (1) | Testi Çöz |
| Test 2 | 7. Sınıf Din Kültürü Testleri (2) | Testi Çöz |
| Test 3 | 7. Sınıf Din Kültürü Testleri (3) | Testi Çöz |
| Test 4 | 7. Sınıf Din Kültürü Testleri (4) | Testi Çöz |
| Test 5 | 7. Sınıf Din Kültürü Testleri (5) | Testi Çöz |
| Test 6 | 7. Sınıf Din Kültürü Testleri (6) | Testi Çöz |
| Test 7 | 7. Sınıf Din Kültürü Testleri (7) | Testi Çöz |
| Test 8 | 7. Sınıf Din Kültürü Testleri (8) | Testi Çöz |
7. Sınıf Din Kültürü ve Ahlak Bilgisi Testleri 8
7. Sınıf Din Kültürü ve Ahlak Bilgisi 8
Kategoriler: Din Kültürü ve Ahlak Bilgisi Etiketler:
7. Sınıf Din Kültürü ve Ahlak Bilgisi Testleri 7
7. Sınıf Din Kültürü ve Ahlak Bilgisi 7
Kategoriler: Din Kültürü ve Ahlak Bilgisi Etiketler: 7. sınıf din kültürü ve ahlak bilgisi testi