5. Sınıf Matematik Doğal Sayılarda Parantezli İşlemler Konu Anlatımı
(3 + 4) – (5 – 3) şeklinde verilen işlem dizisinde parantezin içinde olan işlemler önce yapılır.
Sonuç : (3 + 4) – (5 – 3) = 7 – 2 = 5 tir.
Parantezli işlemlerde, iç içe parantezler varsa, en içteki parantezden başlanarak işlem yapılır.
Örneğin
(8 / (1 + 3)) = (8 / 4) = 2 gibi
İşlem sırası
Karışık işlemlerle karşılaşıldığında önce üslü ifadeler, sonra parantezli ifadeler çözülür.
Örneğin
(23 + 32) + (15 / 2) X 2 = (8 + 9) + (3 X 2) = 17 + 6 = 23
| 5. Sınıf Doğal Sayılarla Parantezli İşlemler | Test Linki |
|---|---|
| 5. Sınıf Matematik Doğal Sayılarla Parantezli İşlemler Konu Anlatımı | Konu Anlatımı |
| 5. Sınıf Matematik Doğal Sayılarla Parantezli İşlemler Çözümlü Sorular | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Parantezli İşlemler Çözümlü Testler | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Parantezli İşlemler Testleri | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Parantezli İşlemler Genel Değerlendirme | Teste Başla |
Kategoriler: Matematik Etiketler:
5. Sınıf Matematik Doğal Sayılarla Çarpma İşlemi Konu Anlatımı
Çarpma İşleminin Tanımı
3 X 5 = 15
Örneğinde gösterilen çarpma işleminde 3 ve 5 çarpan, 15 ise çarpımdır.
Çarpma işlemini;
- 5 + 5 + 5 = 15 şeklinde ifade edersek, çarpmayı toplamanın kısa yoldan yapılması diye tanımlayabiliriz.
Çarpma İşleminin Özellikleri
Örneğin : Aşağıdaki çarpma işlemlerini inceleyiniz.
3 X 5 = 15
5 X 3 = 15
3 X 5 = 5 X 3
Her iki durumda da çarpım aynıdır. Çarpılan iki terimin sırasının değişmesi, çarpımın sonucunu etkilemez.
Örneğin : Aşağıdaki çarpma işlemlerini inceleyiniz.
(2 X 3) X 5 = 6 X 5 = 30
2 X (3 X 5) = 2 X 15 = 30
(2 X 3) X 5 = 2 X (3 X 5) Her iki durumda da çarpım aynıdır.
Üç terimli bir çarpma işleminde ilk iki terimin çarpımı ile üçüncü terimin çarpımı, son iki terimin çarpımı ile ilk iki terimin çarpımı eşit değildir.
Örneğin : Aşağıdaki işlemleri inceleyiniz.
3 X (7 + 5) = 3 X 12 = 36
(3 X 7) + (3 X 5) = 21 + 15 = 36
Sonuç aynı olduğundan;
3 X (7 + 5) = (3 X 7) + (3 X 5)
Bir sayı, toplam halinde olan iki sayı ile toplama yapıldıktan sonra çarpıldığından veya ayrı ayrı çarpılıp toplandığında sonuç değişmez.
| 5. Sınıf Doğal Sayılarla Çarpma İşlemi | Test Linki |
|---|---|
| 5. Sınıf Matematik Doğal Sayılarla Çarpma İşlemi Konu Anlatımı | Konu Anlatımı |
| 5. Sınıf Matematik Doğal Sayılarla Çarpma İşlemi Testleri (1) | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Çarpma İşlemi Test (2) | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Çarpma İşlemi Testi (3) | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Çarpma İşlemi Genel Değerlendirme (4) | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Bölme İşlemi Genel Değerlendirme (5) | Teste Başla |
Kategoriler: Matematik Etiketler:
5. Sınıf Matematik Doğal Sayılarla Çıkarma İşlemi Konu Anlatımı
8 – 5 = 3
Örneğinde gösterilen çıkarma işleminde; 8 eksilen, 5 çıkan, 3 ise farktır.
Örneğin: Aşağıdaki çıkarma işlemlerini inceleyiniz.
7 – 5 = 2
5 – 7 = -2 Aynı değildir.
Eksilen ile çıkanın yerlerinin değişmesi çıkarma işleminin sonucunu etkiler. Eksilen ile çıkanın yerleri değiştirilemez.
Örneğin : Aşağıdaki çıkarma işlemlerini inceleyiniz.
(17 – 10) – 3 = 7 – 3 = 4
17 – (10 – 3) = 17 – 7 = 19 aynı değildir.
Üç terimli bir çıkarma işleminde ilk iki terimin farkı ile üçüncü terimin farkı, son iki terimin farkı ile ilk terimin farkı eşit değildir.
Örneğin : Aşağıdaki çıkarma işlemlerini inceleyiniz.
5 – 0 = 5
12 – 0 = 12
Bir doğal sayıdan “0” ın çıkarılması o sayıyı değiştirmez. Çıkarma işleminde etkisiz eleman sıfırdır.
| 5. Sınıf Doğal Sayılarla Çıkarma İşlemi | Test Linki |
|---|---|
| 5. Sınıf Matematik Doğal Sayılarla Çıkarma İşlemi Konu Anlatımı | Konu Anlatımı |
| 5. Sınıf Matematik Doğal Sayılarla Çıkarma İşlemi Testleri | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Çıkarma İşlemi Test | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Çıkarma İşlemi Testi | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Çıkarma İşlemi Online Test | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Çıkarma İşlemi Genel Değerlendirme | Teste Başla |
Kategoriler: Matematik Etiketler:
5. Sınıf Matematik Doğal Sayılarla Toplama İşlemi Konu Anlatımı
Aynı cinsten varlıkların veya kümeleri bir araya getirerek ileriye doğru yapılan çabuk sayma işlemine TOPLAMA denir.
1- Toplama işleminde terimlerin yerleri değişse de toplam değişmez.
Örnek :
2+3= 5 ve 3+2=5’tir.
2+3 = 3+2
2- Toplama işleminde terimler ikişer ikişer gruplandırılarak toplanırsa, toplam değişmez.
Örnek:
3+4+5=
(3+4)+5= 3+(5+4)=
8+4=12 veya 3+9=21’dir.
(3+5)+4 = 3+(5+4)
3- Toplama işleminde sıfır toplamı, sonucu etkilemez.
Örnek :
5+0=5 ve 0+5=5’tir.
| 5. Sınıf Doğal Sayılarla Toplama İşlemi | Test Linki |
|---|---|
| 5. Sınıf Matematik Doğal Sayılarla Toplama İşlemi Konu Anlatımı | Konu Anlatımı |
| 5. Sınıf Matematik Doğal Sayılarla Toplama İşlemi Testleri (1) | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Toplama İşlemi Test (2) | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Toplama İşlemi Testi (3) | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Toplama İşlemi Online Test (4) | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Toplama İşlemi Test Çöz (5) | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Toplama İşlemi Problemleri (6) | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Toplama İşlemi Soruları (7) | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Toplama İşlemi İle İlgili Sorular (8) | Teste Başla |
| 5. Sınıf Matematik Doğal Sayılarla Toplama İşlemi Genel Değerlendirme (9) | Teste Başla |
Kategoriler: Matematik Etiketler:
Matematik Konu Anlatımı
5. Sınıf Matematik Konu Anlatımı
6. Sınıf Matematik Konu Anlatımı
| Doğal Sayılarla İşlemler | Ondalık Gösterim | Cebirsel İfadeler |
| Üslü Nicelikler | Ondalık Gösterimleri Çözümleme | Örüntü ve İlişkiler |
| İşlem Önceliği | Ondalık Gösterimleri Yuvarlama | Alan Ölçme |
| Doğal Sayıların Çarpanları ve Katları | Ondalık Gösterimlerle Toplama Çıkarma | Paralelkenarın Alanı |
| Bölünebilme Kuralları | Ondalık Gösterimlerle Çarpma Bölme | Üçgenin Alanı |
| Asal Sayılar | Veri Toplama ve Düzenleme | Arazi Ölçme Birimleri |
| Açılar | Aritmetik Ortalama ve Açıklık | Prizmaların Hacmi |
| Oran Orantı | Tam Sayılar | Hacim Ölçme Birimleri |
| Toplama Çıkarma | Mutlak Değer | Prizmaların Hacmini Hesaplama |
| Çarpma Bölme | Tam Sayılarla Toplama ve Çıkarma | Sıvıları Ölçme |
7. Sınıf Matematik Konu Anlatımı
8. Sınıf Matematik Konu Anlatımı
Kategoriler: Matematik, Matematik, Matematik, Matematik Etiketler: 5 matematik konu anlatımı, 6 matematik konu anlatımı, 7 matematik konu anlatımı, 8 matematik konu anlatımı
5. Sınıf Matematik Örüntüler Konu Anlatımı
Kuralında Bir İşlem Bulunan Bir Örüntü Oluşturma
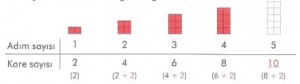
1. Aşağıdaki örüntünün her adımında kaç tane kare olduğunu yazalım.
Karelerin hangi sayısal ilişkiye göre dizildiğini ve beşince adımda kaç tane kare olması gerektiğini bulalım:
Bilgi : Bir örüntüyü devam ettirebilmek için önce örüntünün kuralını bulmamız gerekir. Yukarıdaki örüntüde, karelerin sayısı her adımda 2 artarak devam ediyor.
5. adımda; 8+2 = 10 kare olmalıdır.
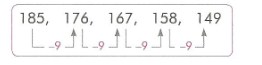
2. 109,100,91,82, … sayı örüntüsünü hangi sayı devam ettirir?
Kural : Örüntü, 109’dan başlayıp 9 eksilerek devam ediyor.
Kuralı uygulayalım : 82-9=73
Yukarıdaki örüntünün kuralına uygun, ilk sayısı 185 olan bir örüntü oluşturalım:
Aşağıda verilen kurallara göre sayı örüntüleri oluşturunuz.
Örüntü kuralı +75 -> 25, … , … , … , … , … , …
Örüntü kuralı X2 -> 2, … , … , … , … , … , …
Örüntü kuralı -25 -> 925, … , … , … , … , … , …
Örüntü kuralı : 2 -> 1600, … , … , … , … , … , …
Problem Çözme
Aşağıdaki problemlerin çözümünü bir örüntü oluşturarak bulunuz.
1. Bir otomobil, 1 L benzin ile 12 km yol gidiyor. Bu otomobil 8 L benzin ile kaç kilometre yol gidebilir.
2. Her gün 3 TL biriktirsem, 42 TL’yi kaç günde biriktiririm?
Bir Örüntüyü Kuralına Göre Devam Ettirme
Aşağıdaki sayı örüntüsünü hangi sayı devam ettirir?
126,120,114, 108, =
Kuralı bulalım : Örüntü, 126’dan başlayıp 6 eksilerek devam ediyor.
Kuralı uygulayalım : 108 – 6 = 102
Örüntüyü devam ettirecek sayı 102’dir.
Bir Örüntüde Eksik Olan Sayıları Bulma
Aşağıdaki örüntüde boş bırakılan yerlere hangi sayılar gelmelidir?
181, 201, 221, ?, ?, 301
Kuralı bulalım : Örüntü, 181’den başlayıp 20 artarak devam ediyor.
Kuralı uygulayalım : 241 + 20 = 261, 261 + 20 = 281
Örüntüdeki boş yerlere sırayla, 261 ve 281 sayıları gelmelidir.
Bir Örüntüde Kuralı Bozan Sayıyı Bulma
Aşağıdaki örüntüde, kuralı bozan sayı yerine hangi sayı gelmelidir?
1, 3, 9, 27, 81, 263, 729
Kuralı bulalım : Örüntü 1’den başlayıp, bir önceki sayının 3 katı alınarak devam ediyor.
Kuralı uygulayalım : 81X3 = 263 yanlış
81 X 3 = 243 doğru
Örüntüdeki 263 doğal sayısının yerine 243 gelmelidir.
Kategoriler: Matematik Etiketler: